题目内容
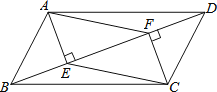
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

【答案】(1)证明见解析;(2)36m2;(3)P 的坐标为(0,-2)或(0,10).
【解析】
(1)先根据勾股定理求出 BD 的长度,然后根据勾股定理的逆定理,即可证明
BD⊥BC;
(2)根据四边形 ABCD 的面积=△ABD 的面积+△BCD 的面积,代入数据计算即可求解;
(3)先根据 S△PBD=![]() S四边形 ABCD,求出 PD,再根据 D 点的坐标即可求解.
S四边形 ABCD,求出 PD,再根据 D 点的坐标即可求解.
(1)证明:连接 BD.
∵AD=4m,AB=3m,∠BAD=90°,
∴BD=5m.
又∵BC=12m,CD=13m,
∴BD2+BC2=CD2.
∴BD⊥CB;
(2)四边形 ABCD 的面积=△ABD 的面积+△BCD 的面积
=![]() ×3×4+
×3×4+ ![]() ×12×5
×12×5
=6+30
=36(m2).
故这块土地的面积是 36m2;
(3)∵S△PBD=![]() S 四边形ABCD
S 四边形ABCD
∴![]() PDAB=
PDAB=![]() ×36,
×36,
∴![]() PD×3=9,
PD×3=9,
∴PD=6,
∵D(0,4),点 P 在 y 轴上,
∴P 的坐标为(0,-2)或(0,10).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目