题目内容
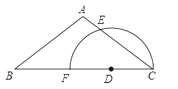
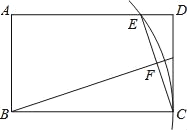
【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】试题分析:首先根据以B为圆心BC为半径画弧交AD于点E,判断出AE=BC=5;然后根据勾股定理,求出AE的值是多少,进而求出DE的值是多少;再根据勾股定理,求出CE的值是多少,再根据BC=BE,BF⊥CE,判断出点F是CE的中点,据此求出CF、BF的值各是多少;最后根据角的正切的求法,求出tan∠FBC的值是多少即可.
试题解析:∵以B为圆心BC为半径画弧交AD于点E,
BE=BC=5,
∴AE=![]() ,
,
∴DE=AD-AE=5-4=1,
∴CE=![]()
∵BC=BE,BF⊥CE,
∴点F是CE的中点,
∴CF=![]() CE=
CE=![]() ,
,
∴BF=![]()
∴tan∠FBC=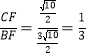
即tan∠FBC的值为![]() .
.
故选D.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目