题目内容
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作等边
的右侧作等边![]() .
.
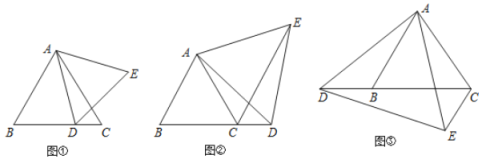
(1)如图①,点![]() 在线段
在线段![]() 上移动时,直接写出
上移动时,直接写出![]() 和
和![]() 的大小关系;
的大小关系;
(2)如图②,点![]() 在线段
在线段![]() 的延长线上移动时,猜想
的延长线上移动时,猜想![]() 的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,不发生变化;理由见解析
,不发生变化;理由见解析
【解析】
(1)由等边三角形的性质得出∠BAC=∠DAE,容易得出结论;
(2)由△ABC和△ADE是等边三角形可以得出AB=BC=AC,AD=AE,∠ABC=∠ACB=∠BAC=∠DAE=60°,得出∠ABD=120°,再证明△ABD≌△ACE,得出∠ABD=∠ACE=120°,即可得出结论.
解:(1)![]() ;理由如下:
;理由如下:
∵![]() 和△
和△![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ;
;
(2)![]() ,不发生变化;理由如下:
,不发生变化;理由如下:
∵![]() 是等边三角形,
是等边三角形,![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
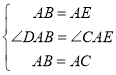 ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目