题目内容
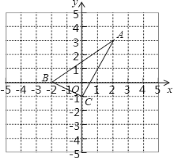
【题目】已知平面直角坐标系中两定点![]() 、
、![]() ,抛物线
,抛物线![]() 过点A,B,与y交于C点,点P(m,n)为抛物线上一点.
过点A,B,与y交于C点,点P(m,n)为抛物线上一点.
(1)求抛物线的解析式和点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)当∠PAB=∠ABC时,求点P的坐标.
【答案】解:(1)∵抛物线![]() 过点A,B,
过点A,B,
∴![]() ,解得:
,解得:  ,
,
∴抛物线的解析式为: ![]() .
.
∴C![]() .
.
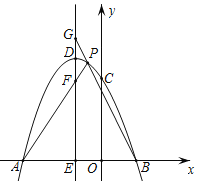
(2)以AB为直径作圆M,与y轴交于点P.则抛物线在圆内的部分,能使∠APB为钝角,
∴M(![]() ,0),⊙M的半径=
,0),⊙M的半径=![]() .
.
∵P是抛物线与y轴的交点,
∴OP=2,
∴MP=![]()
∴P在⊙M上,
∴由抛物线的对称性可知, ![]() ,
,
∴当-1<m<0或3<m<4时,∠APB为钝角.
(3)在Rt△OBC中, ![]() .
.
第一种情况:过A作AP∥BC,交抛物线于点P .

∴∠PAB=∠ABC.
过P作PQ⊥AB于Q,
∴![]() .
.
∵P(m,n),
∴PQ=n,AQ=m+1
∴![]() .
.
∴![]() .
.
解得![]()
∴![]()
第二种情况:点P关于x轴的对称点的坐标为![]()
∴直线AP″的解析式为![]()
∴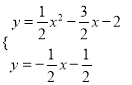 解得
解得![]()
∴![]()
∴![]()
【解析】试题(1)将A点,B点坐标代入解析式,即可求出解析式,可得 C点坐标;(2)以AB为直径作圆M,与y轴交于点P.因为AB为直径,所以当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,根据题意可证得P在⊙M上,由抛物线的对称性可知, ![]() ,可得-1<m<0,或3<m<4;(3)根据题意分两种情况进行讨论,即可得出答案.
,可得-1<m<0,或3<m<4;(3)根据题意分两种情况进行讨论,即可得出答案.

练习册系列答案
相关题目