Question

【题目】如图，圆⊙O的半径为1，等腰直角三角形ABC的顶点B的坐标为（2，0），∠CAB=90°，AC=AB，顶点A在⊙O上运动，当直线AB与⊙O相切时，A点的坐标为____________．

Answer 1

【答案】() ，()

【解析】

相切时有两种情况，在第一象限或者第四象限，连接OA，并过点A作AE⊥OB于点E，在Rt△OAE中求出OE，然后就能求出A点坐标．

①、当点 A 位于第一象限时：

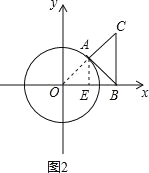
连接 OA ，并过点 A 作 AE⊥OB 于点 E ，

∵ 直线 AB 与 ⊙O 相切，∴∠OAB=90°， 又 ∵∠CAB=90°，∴∠CAB+∠OAB=180°，

∴ 点 O 、A. C 在同一条直线上，∵OB=2OA ，∴∠ABO=30°，∠AOB=60°，

∴OE=OA=，AE=OE=， 点A的坐标为 (，) ；

②、当点A位于第四象限时，根据对称性可知点A的坐标为(，)；

综上所述 , 点 A 的坐标为(，)或(，)；