题目内容
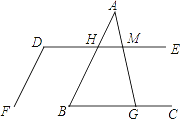
【题目】如图,四边形ABCD,![]() ,
,![]() ,连接BD.
,连接BD.

(1)如图1,求证DB平分![]() ;
;
(2)如图2,连接AC,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,延长AD交BC的延长线于F,点E在边AB上,![]() ,连CE交BD于G,当
,连CE交BD于G,当![]() ,
,![]() 时,求BD的长.
时,求BD的长.
【答案】(1)见解析;(2)见解析;(3)7
【解析】
(1)过B作BE⊥AD于E,过B作BF⊥DC于F.根据四边形内角和为360°得到∠A+∠DCB=180°.再根据同角的补角相等得到∠A=∠FCB.即可证明△AEB≌△CFB,得到BE=BF,根据到角两边距离相等的点在角平分线上即可得到结论;
(2)如图2中,在BD截取DE=AD,连接AE,首先证明△ADE是等边三角形,只要证明△DAC≌△EAB(SAS),即可解决问题;
(3)如图3中,作EN∥DC交BD于N,在DF上截取DM=DC.想办法证明△CFM≌△EBN(AAS),△DGC≌△NGE(AAS),即可解决问题.
(1)如图1.过B作BE⊥AD于E,过B作BF⊥DC于F.
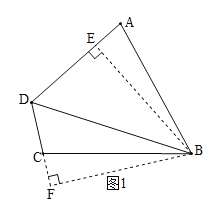
∵∠ABC+∠ADC=180°,∴∠A+∠DCB=180°.
∵∠DCB+∠FCB=180°,∴∠A=∠FCB.
∵BE⊥AD,BF⊥DC,∴∠AEB=∠CFB=90°.
在△AEB和△CFB中,∵∠A=∠FCB,∠AEB=∠CFB=90°,AB=CB,
∴△AEB≌△CFB,
∴BE=BF.
∵BE⊥AD,BF⊥DC,BE=BF,∴DB平分∠ADC;
(2)如图2中,在BD截取DE=AD,连接AE,
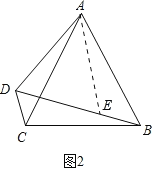
∵AB=CB,∠BAC=60°,∴△ABC是等边三角形,∴∠ABC=60°.
∵∠ABC+∠ADC=180°,∴∠ADC=120°.
由(1)得:DB平分∠ADC,∴∠ADB=∠CDB=60°.
∵DE=AD,∴△ADE是等边三角形,∴AD=DE=AE.
∵∠DAE=∠CAB=60°,∴∠DAC=∠BAE,
在△DAC与△EAB中,∵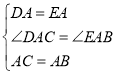 ,
,
∴△DAC≌△EAB(SAS),∴DC=BE.
∵BD=BE+DE,∴BD=AD+CD,
即BD﹣CD=AD.
(3)作EN∥DC交BD于N,在DF上截取DM=DC.
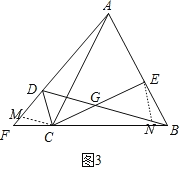
∵∠ADC=120°,∴∠CDM=60°.
∵DM=DC,∴△DMC是等边三角形,
∴CM=CD=DM,∠DMC=60°,∴∠FMC=120°.
∵CD∥EN,∴∠CDG=∠ENG=60°,
∴∠ENB=120°,∴∠CMF=∠ENB.
∵∠F+∠FBD=∠ADB=60°,∠FBD+∠EBN=60°,
∴∠F=∠EBN.
在△CFM和△EBN中,∵∠CMF=∠ENB,∠F=∠EBN,CF=BE,
∴△CFM≌△EBN(AAS),∴FM=BN,EN=CM=CD.
∵EN∥CD,∴∠CDG=∠GNE.
∵∠DGC=∠EGN,∴△DGC≌△NGE(AAS),
∴DG=GN=3,∴2BD=AF﹣FM+DN+BN=8+6=14,∴BD=7.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案