��Ŀ����
����Ŀ����ͼ��CD�Ǿ�����BCA�Ķ���C��һ��ֱ�ߣ�CA��CB��E��F��ֱ��CD�ϵ����㣬�ҡ�BEC����CFA����.
(1)��ֱ��CD������BCA���ڲ�����E��F������CD�ϣ����������������⣺
����ͼ(a)������BCA��90�㣬����90������BE________CF��EF________|BE��AF|(����>����<����������)��
����ͼ(b)����0�㣼��BCA��180����������һ�����������BCA��ϵ������________��ʹ���е�����������Ȼ��������֤���������۳�����
(2)��ͼ(c)����ֱ��CD������BCA���ⲿ����BCA��������д��EF��BE��AF�����߶�������ϵ�ĺ�������(��Ҫ��֤��)��

���𰸡�(1)����������������������ǣ�������BCA��180��.֤����������(2)EF��BE��AF.
��������
(1)�������BEC=��AFC=90�㣬��CBE=��ACF������AAS֤��BCE�ա�CAF���Ƴ�BE=CF��CE=AF���ɣ��������BEC=��AFC����CBE=��ACF������AAS֤��BCE�ա�CAF���Ƴ�BE=CF��CE=AF����
(2)�����BEC=��AFC����CBE=��ACF������AAS֤��BCE�ա�CAF���Ƴ�BE=CF��CE=AF����.
�⣺(1)����ͼ��E����F�����࣬
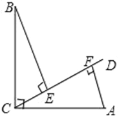
��BE��CD��AF��CD����ACB=90�㣬
���BEC=��AFC=90�㣬
���BCE����ACF=90�㣬��CBE+��BCE=90�㣬
���CBE=��ACF��
�ڡ�BCE�͡�CAF��
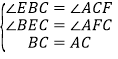 ��
��
���BCE�ա�CAF(AAS)��
��BE=CF��CE=AF��
��EF=CF��CE=BE��AF��
��E��F���Ҳ�ʱ��ͬ����֤EF=AF��BE��
��EF=|BE��AF|��
�ڡϦ�����ACB=180��ʱ����������������Ȼ������
֤�����ߡ�BEC=��CFA=��a���Ϧ�����ACB=180�㣬
���CBE=��ACF��
�ڡ�BCE�͡�CAF��
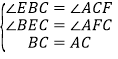 ��
��
���BCE�ա�CAF��AAS����
��BE=CF��CE=AF��
��EF=CF��CE=BE��AF��
��E��F���Ҳ�ʱ��ͬ����֤EF=AF��BE��
��EF=|BE��AF|��
(2)EF=BE��AF
�����ǣ��ߡ�BEC=��CFA=��a����a=��BCA��
�֡ߡ�EBC+��BCE+��BEC=180�㣬��BCE+��ACF+��ACB=180�㣬
���EBC+��BCE=��BCE+��ACF��
���EBC=��ACF��
�ڡ�BEC�͡�CFA��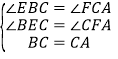 ��
��
���BEC�ա�CFA(AAS)��
��AF=CE��BE=CF��
��EF=CE��CF��
��EF=BE��AF.