题目内容
【题目】已知命题“等腰三角形两腰上的高线长相等”
（1）请写出该命题的逆命题；
（2）判断（1）中命题的真假，并画出图形，补充已知，求证，及证明过程．
图形：
已知：在△ABC中，CD⊥AB，BE⊥AC，且______．
求证：______．
证明：
【答案】(1)见解析;(2)见解析.
【解析】
（1）根据原命题和逆命题的关系，即调换条件和结论；
（2）根据（1）的条件和结论写出已知和求证，再画出图形，然后结合图形证明Rt△AEBE≌RtADC，证得AB=AC，即为等腰三角形.
解：（1）逆命题是如果一个三角形两条边上的高相等，那么这个三角形是等腰三角形；；
（2）已知：在△ABC中，CD⊥AB，BE⊥AC，且CD=BE，
求证：△ABC是等腰三角形．
证明：如图，
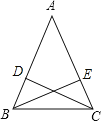
∵BE、CD是△ABC的高，
∴CD⊥AB，BE⊥AC，
∵∠A=∠A，
∵BE=CD，
∴Rt△AEB≌Rt△ADC（AAS），
∴AB=AC，
∴△ABC是等腰三角形．
练习册系列答案
阅读快车系列答案
相关题目
【题目】踏春时节，某班学生集体组织亲子游，沿着瓯江口樱花步道骑自行车，该班学生花了950元租了若干辆自行车，已知自行车的类型和租车价格如下表：
自行车类型 |
|
|
|
座位教（个） | 2 | 3 | 4 |
租车价格（元/辆） | 30 | 45 | 55 |
（1）若同时租用
、
两种类型的车，且共有65个座位，则应租、类型车各多少辆？
（2）若型车租4辆，余下的租用
型和型，要求每种车至少租用1辆，请你帮他们设计型车和型车的租车方案．
（3）若同时租用这三类车，且每种车至少租用1辆，则最多能租到______个座位．（直接写出答案）
