题目内容
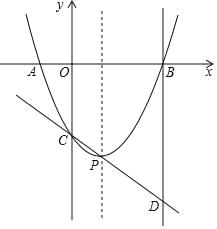
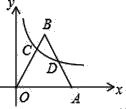
【题目】如图，在平面直角坐标系中，等边三角形OAB的顶点A的坐标为（5，0），顶点B在第一象限，函数y=
（x＞0）的图象分别交边OA、AB于点C、D．若OC=2AD，则k=_____
【答案】4
【解析】
作CE⊥x轴于点E，DF⊥x轴于点F， CE=2DF；设OE为a，则CE=
；由反比例函数k的几何意义可知△COE与△AOD面积相等，则因OC=2AD可得OF=2a；再由C和D点均在反比例函数上可求解k.
解：作CE⊥x轴于点E，DF⊥x轴于点F，
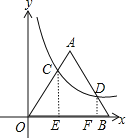
设OE为a，由题意可知△AOB为等边三角形可得CE=，则DF=
，BF=
；由反比例函数k的几何意义可知△COE与△AOD面积相等，则由三角形面积公式及CE=2DF可得OF=2OE=2a；由OB=5可得OF+BF=2a+=5，解得a=2，则k=2×2=4.
故答案为：4.
【题目】在一个不透明的袋子中装有除颜色外其余均相同的m个小球，其中 5 个黑球， 从袋中随机摸出一球，记下其颜色，这称为依次摸球试验，之后把它放回袋 中，搅匀后，再继续摸出一球．以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表：
摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次数 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
根据列表，可以估计出 m 的值是（ ）
A. 5 B. 10 C. 15 D. 20
【题目】甲、乙两名队员参加设计训练，成绩分别被制成下列两个统计图：
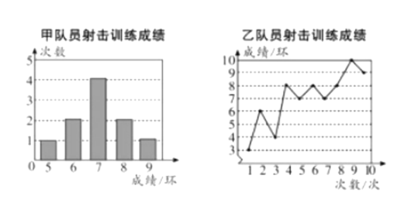
根据以上信息，整理分析数据如下：
平均数（环） | 中位数（环） | 众数（环） | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
（1）表格中
，
，
；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩，若选派其中一名参赛，你认为应选哪名队员？
（3）如果乙再射击
次，命中
环，那么乙的射击成绩的方差 ．（填“变大”“变小”或“不变”）
