题目内容
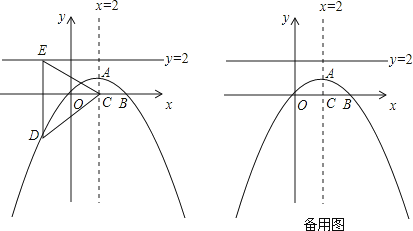
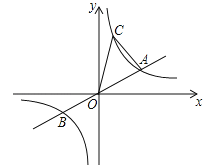
【题目】如图,已知:直线![]() 与双曲线
与双曲线![]() 交于A.B两点,且点A的横坐标为4, 若双曲线
交于A.B两点,且点A的横坐标为4, 若双曲线![]() 上一点C的纵坐标为8,连接AC.
上一点C的纵坐标为8,连接AC.
(1)填空: k的值为_______; 点B的坐标为___________;点C的坐标为___________.
(2)直接写出关于的不等式![]() 的解集.
的解集.
(3)求三角形AOC的面积
(4) 若在x轴上有点M,y轴上有点N,且点M.N.A.C四点恰好构成平行四边形,直接写出点M.N的坐标.
【答案】(1)k=8 ,B(-4,-2),C(1,8) ;(2)![]() ;(3) 15;(4)M(3,0)、N(0,6)或M(-3,0)、N(0,-6)
;(3) 15;(4)M(3,0)、N(0,6)或M(-3,0)、N(0,-6)
【解析】分析:(1)由直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点横坐标为4,代入正比例函数,可求得点A的坐标,继而求得k值,把C的纵坐标代入反比例函数,即可得到C的坐标;根据对称性,可求得点B的坐标.
交于A、B两点,A点横坐标为4,代入正比例函数,可求得点A的坐标,继而求得k值,把C的纵坐标代入反比例函数,即可得到C的坐标;根据对称性,可求得点B的坐标.
(2)结合图象,即可求得关于x的不等式![]() 的解集;
的解集;
(3)首先过点C作CD⊥x轴于点D,过点A作AE⊥轴于点E,可得S△AOC=S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC,又由双曲线![]() 上有一点C的纵坐标为8,可求得点C的坐标,继而求得答案;
上有一点C的纵坐标为8,可求得点C的坐标,继而求得答案;
(4)由当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形,根据平移的性质,即可求得答案.
详解:(1)∵直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点横坐标为4,∴点A的纵坐标为:y=
交于A、B两点,A点横坐标为4,∴点A的纵坐标为:y=![]() ×4=2,∴点A(4,2),∴2=
×4=2,∴点A(4,2),∴2=![]() ,∴k=8,∴
,∴k=8,∴![]() ;把y=8代入
;把y=8代入![]() ,解得:x=1,∴C(1,8).
,解得:x=1,∴C(1,8).
∵直线![]() 与双曲线
与双曲线![]() 交于A、B两点,∴B(﹣4,﹣2);
交于A、B两点,∴B(﹣4,﹣2);
(2)由图象可知:关于x的不等式![]() 的解集为:﹣4≤x<0或x≥4;
的解集为:﹣4≤x<0或x≥4;
(3)过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E.
∵双曲线![]() 上有一点C的纵坐标为8,∴把y=8代入y=
上有一点C的纵坐标为8,∴把y=8代入y=![]() ,得:x=1,∴点C(1,8),∴S△AOC=S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC=
,得:x=1,∴点C(1,8),∴S△AOC=S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC=![]() ×(2+8)×(4﹣1)=15;
×(2+8)×(4﹣1)=15;
(4)如图,当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形.
∵点A(4,2),点C(1,8),∴根据平移的性质可得:M(3,0),N(0,6)或M′(﹣3,0),N′(0,﹣6).


 阅读快车系列答案
阅读快车系列答案