题目内容
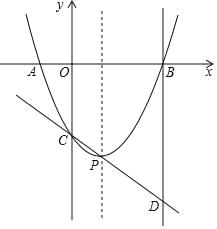
【题目】如图,二次函数 y=ax2﹣2ax+c(a>0)的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点,与 y 轴交于点 C,它的顶点为 P,直线 CP 与过点B 且垂直于 x 轴的直线交于点 D,且 CP:PD=1:2,tan∠PDB=![]() .
.
(1)则 A、B 两点的坐标分别为 A( , ); B( , );
(2)求这个二次函数的解析式;
(3)在抛物线的对称轴上找一点M 使|MC﹣MB|的值最大,则点M 的坐标为 .
【答案】(1)﹣1,0;3,0;(2)y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ;(3)(1,﹣
;(3)(1,﹣![]() )
)
【解析】
(1)先求得抛物线的对称轴为x=1,然后利用平行线分线段成比例定理求得OE:EB的值,从而得到点B的坐标,利用抛物线的对称性可求得点A的坐标;
(2)过点C作CF⊥PE,垂足为F.先求得点C和点P的坐标(用含字母的式子表示),然后可得到PF=a,然后利用锐角三角函数的定义可求得a的值,然后将点A和点B的坐标代入抛物线的解析式可求得c的值;
(3)根据三角形的任意两边之差小于第三边判断出点A、C、M在同一直线上时|MC-MB|最大,设直线AC的解析式为y=kx+b,利用待定系数法求出一次函数解析式,再根据点M在对称轴上代入计算即可得解.
(1)如图所示:
∵由题意可知:抛物线的对称轴为x=1,
∴OE=1.
∵OC∥PE∥BD,CP:PD=1:2,
∴![]() =
=![]() .
.
∴BE=2.
∴OB=3.
∴B(3,0).
∵点A与点B关于PE对称,
∴点A的坐标为(﹣1,0).
故答案是:﹣1,0;3,0;
(2)过点C作CF⊥PE,垂足为F.
将x=0代入得:y=c,
∴点C的坐标为(0,c).
将x=1代入得y=﹣a+c.
∴点P的坐标为(1,﹣a+c).
∴PF=a.
∵PE∥BD,tan∠PDB=![]() ,
,
∴tan∠CPF=tan∠PDB=![]() .
.
∴![]() .
.
解得a=![]() .
.
将a=![]() 代入抛物线的解析式得:y=
代入抛物线的解析式得:y=![]() x2﹣
x2﹣![]() x+c.
x+c.
将点A的坐标代入得:![]() +
+![]() +c=0,解得:c=﹣
+c=0,解得:c=﹣![]() .
.
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() .
.
(3)由三角形的三边关系,|MC﹣MB|<AC,
∴当点A、C、M在同一直线上时|MC﹣MB|最大,
设直线AC的解析式为y=kx+b,
则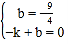 ,
,
解得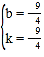 ,
,
∴y=﹣![]() x﹣
x﹣![]() ,
,
∵抛物线对称轴为直线x=1,
∴当x=1时,y=﹣![]() ×1﹣
×1﹣![]() =﹣
=﹣![]() ,
,
∴点M的坐标为(1,﹣![]() ).
).
故答案是:(1,﹣![]() ).
).

【题目】山西省地处中纬度,属于温带大陆性气候,因此适合种植玉米、高粱、大豆、花生等农作物,农民李大叔有一块总面积为![]() 的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:


农作物 | 占地面积( | 产量(千克/垄) | 利润(元/千克) |
玉米 | 30 | 60 | 0.5 |
高粱 | 20 | 50 | 0.8 |
(1)若设高粱种植了![]() 垄,请说明共有几种种植方案,分别是哪几种;
垄,请说明共有几种种植方案,分别是哪几种;
(2)在以上种植方案中,哪种方案获得的利润最大?最大利润是多少?