题目内容
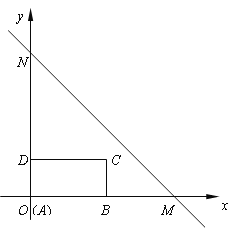
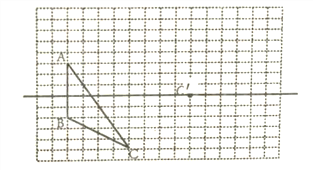
【题目】如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(﹣1,0),点C与点B关于x轴对称,连接AB、AC.
(1)求过A、B、D三点的抛物线的解析式;
(2)有一动点E从原点O出发,以每秒2个单位的速度向右运动,过点E作x轴的垂线,交抛物线于点P,交线段CA于点M,连接PA、PB,设点E运动的时间为t(0<t<4)秒,求四边形PBCA的面积S与t的函数关系式,并求出四边形PBCA的最大面积;
(3)抛物线的对称轴上是否存在一点H,使得△ABH是直角三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)S=﹣8t2+32t+32,当t=2时,S有最大值,且最大值为64;(3)H(
;(2)S=﹣8t2+32t+32,当t=2时,S有最大值,且最大值为64;(3)H(![]() ,11),(
,11),(![]() ,
, ![]() ).
).
【解析】试题分析:(1)由于A(8,0),D(﹣1,0),故设过A、B、D三点的抛物线的解析式为y=a(x+1)(x﹣8),将B(0,4)代入即可求得a,进而求得抛物线的解析式为;
(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由(![]() PQOA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值;
PQOA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值;
(3)根据已知条件得到∠HAB<90°,①当∠ABH=90°时,求得直线AB:y=﹣![]() x+4,直线BH:y=2x+4,于是得到H(
x+4,直线BH:y=2x+4,于是得到H(![]() ,11),②当∠AHB=90°时,过B作BN⊥对称轴于N,则BN=
,11),②当∠AHB=90°时,过B作BN⊥对称轴于N,则BN=![]() ,AG=
,AG=![]() ,设对称轴交x轴于G,根据相似三角形的性质得到HN=
,设对称轴交x轴于G,根据相似三角形的性质得到HN=![]() (负值舍去),于是得到H(
(负值舍去),于是得到H(![]() ,
, ![]() ).
).
(1)∵A(8,0),D(﹣1,0),设过A、B、D三点的抛物线的解析式为y=a(x+1)(x﹣8),将B(0,4)代入得﹣8a=4,∴a=﹣![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ,即
,即![]() ;
;
(2)△ABC中,AB=AC,AO⊥BC,则OB=OC=4,![]() x+4;依题意,知:OE=2t,即 E(2t,0);∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;S=S△ABC+S△PAB=
x+4;依题意,知:OE=2t,即 E(2t,0);∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;S=S△ABC+S△PAB=![]() ×8×8+
×8×8+![]() ×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;∴当t=2时,S有最大值,且最大值为64;
×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;∴当t=2时,S有最大值,且最大值为64;
(3)存在,∵抛物线的对称轴为:x=![]() =
=![]() ,∵直线x=
,∵直线x=![]() 垂直x轴,∴∠HAB<90°,①当∠ABH=90°时,由A(8,0)、B(0,4),得:直线AB:y=﹣
垂直x轴,∴∠HAB<90°,①当∠ABH=90°时,由A(8,0)、B(0,4),得:直线AB:y=﹣![]() x+4,所以,直线BH可设为:y=2x+h,代入B(0,4),得:h=4,∴直线BH:y=2x+4,当x=
x+4,所以,直线BH可设为:y=2x+h,代入B(0,4),得:h=4,∴直线BH:y=2x+4,当x=![]() 时,y=11,∴H(
时,y=11,∴H(![]() ,11),②当∠AHB=90°时,过B作BN⊥对称轴于N,则BN=
,11),②当∠AHB=90°时,过B作BN⊥对称轴于N,则BN=![]() ,AG=
,AG=![]() ,设对称轴交x轴于G,∵∠AHG=∠HBN=90°﹣∠BHN,∠BNH=∠AGH=90°,∴△AHG∽△BHN,∴
,设对称轴交x轴于G,∵∠AHG=∠HBN=90°﹣∠BHN,∠BNH=∠AGH=90°,∴△AHG∽△BHN,∴![]() ,∴
,∴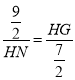 ,∴HN(HN+4)=
,∴HN(HN+4)=![]() ,∴4(HN)2+16HN﹣63=0,解得:HN=
,∴4(HN)2+16HN﹣63=0,解得:HN=![]() (负值舍去),∴H(
(负值舍去),∴H(![]() ,
, ![]() ),综上所述,H(
),综上所述,H(![]() ,11),(
,11),(![]() ,
, ![]() ).
).