题目内容
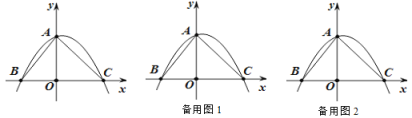
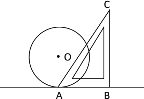
【题目】如图，半径为2的圆O与含30°角的直角三角板ABC的AB边切于点A，将直角三角板沿BA边所在的直线向右平移，当平移到AC与圆O相切时，该直角三角板的平移距离为（ ）
A. 
B. 
C. 1D. 2
【答案】B
【解析】
作出平移后的图形，根据切线的性质证得△OAD是等边三角形，再根据切线长定理得A’D=A A’，然后利用三角函数求出A’D,即可求出平移的距离.
解：如图，三角板ABC平移后的AC的对应边为A’C’,与⊙O切于点D.
易知OA⊥AB,OD⊥A’C’,AC∥A’C’,△OAD是等边三角形.
∴AD=OA=2, A’D=A A’,
∵∠DAE=∠OAB-∠CAB=90°-60°=30°
∴DE=
AD=1
∴A’D=
=
∴A A’=即平移的距离为.
故选：B
练习册系列答案
相关题目
