题目内容
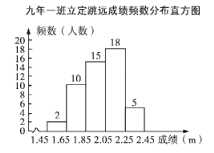
【题目】在阳光大课间活动中,某校开展了立定跳远、实心球、长跑等体育活动,为了了解九年一班学生的立定跳远成绩的情况,对全班学生的立定跳远测试成绩进行统计,并绘制了以下不完整的频数分布直方图和扇形图,根据图中信息解答下列问题.

(1)求九年一班学生总人数,并补全频数分布直方图(标注频数);
(2)求2.05≤a<2.25成绩段在扇形统计图中对应的圆心角度数;
(3)直接写出九年一班学生立定跳远成绩的中位数所在的成绩段;
(4)九年一班在2.25≤a<2.45成绩段中有男生3人,女生2人,现要从这5人中随机抽取2人参加学校运动会,请用列表法或树状图法求出恰好抽到一男一女的概率.
【答案】(1)50人,补全频数分布直方图,如下图所示:见解析;(2)129.6°;(3)1.85≤a<2.05;(4)恰好抽到一男一女的概率为0.6.
【解析】
(1))结合直方图和扇形统计图得知成绩在1.85-2.05段的学生有15人,占30%可得九一年总人数并补全直方图;(2)先求出成绩在2.05≤a<2.25段中的人数,及占的百分比,用360°乘以这个百分比即可;(3)由中位数定义可找到第25,26个同学所在的段可得到中位数所在的成绩段;(4)用列表法列出所有可能出现的情况,恰好抽到一男一女的情况,再用概率公式求出其概率即可.
(1)结合直方图和扇形统计图,全班总人数为:15÷30%=50(人),
2.05≤a<2.25成绩段中的人数:50-(2+10+15+5)=50-22=18(人).
补全频数分布直方图,如下图所示:
(2)2.05≤a<2.25成绩段在扇形统计图中对应的圆心角度数:360°×![]() =129.6°.
=129.6°.
(3)全班50人,按从小到大排列第25-26名在1.85≤a<2.05组,所以中位数所在的成绩段在1.85≤a<2.05;
(4)用A1、A2、A3分别表示3个男生,B1、B2分别表示两个女生,可列表如下:
A1 | A2 | A3 | B1 | B2 | |
A1 | (A1,A2) | (A1,A3) | (A1,B1) | (A1,B2) | |
A2 | (A2,A1) | (A2,A3) | (A2,B1) | (A2,B2) | |
A3 | (A3,A1) | (A3,A2) | (A3,B1) | (A3,B2) | |
B1 | (B1,A1) | (B1,A2) | (B1,A3) | (B1,B2) | |
B2 | (B2,A1) | (B2,A2) | (B2,A3) | (B2,B1) |
由表格可知,所有可能出现的情况一共有20种,恰好抽到一男一女的情况有12种,
所以恰好抽到一男一女的概率为![]() =0.6.
=0.6.