题目内容
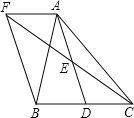
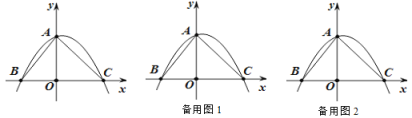
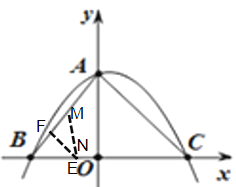
【题目】如图,抛物线y=ax2+bx+4(a≠0)与![]() 轴交于点B (-3 ,0) 和C (4 ,0)与
轴交于点B (-3 ,0) 和C (4 ,0)与![]() 轴交于点A.
轴交于点A.
(1) a = ,b = ;
(2) 点M从点A出发以每秒1个单位长度的速度沿AB向B运动,同时,点N从点B出发以每秒1个单位长度的速度沿BC向C运动,当点M到达B点时,两点停止运动.t为何值时,以B、M、N为顶点的三角形是等腰三角形?
(3) 点P是第一象限抛物线上的一点,若BP恰好平分∠ABC,请直接写出此时点P的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)直接利用待定系数法求二次函数解析式得出即可;
(2)分三种情况:①当BM=BN时,即5-t=t,②当BM=NM=5-t时,过点M作ME⊥OB,因为AO⊥BO,所以ME∥AO,可得:![]() 即可解答;③当BE=MN=t时,过点E作EF⊥BM于点F,所以BF=
即可解答;③当BE=MN=t时,过点E作EF⊥BM于点F,所以BF=![]() BM=
BM=![]() (5-t),易证△BFE∽△BOA,所以
(5-t),易证△BFE∽△BOA,所以![]() 即可解答;
即可解答;
(3)设BP交y轴于点G,过点G作GH⊥AB于点H,因为BP恰好平分∠ABC,所以OG=GH,BH=BO=3,所以AH=2,AG=4-OG,在Rt△AHG中,由勾股定理得:OG=![]() ,设出点P坐标,易证△BGO∽△BPD,所以
,设出点P坐标,易证△BGO∽△BPD,所以![]() ,即可解答.
,即可解答.
解:解:(1)∵抛物线过点B (-3 ,0) 和C (4 ,0),
∴![]() ,
,
解得: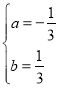 ;
;
(2)∵B (-3 ,0),y=ax2+bx+4,∴A(0,4),0A=4,OB=3,
在Rt△ABO中,由勾股定理得:AB=5,
t秒时,AM=t,BN=t,BM=AB-AM=5-t,
①如图:当BM=BN时,即5-t=t,解得:t=![]() ;
;
, 
②如图,当BM=NM=5-t时,过点M作ME⊥OB,因为BN=t,由三线合一得:BE=![]() BN=
BN=![]() t,又因为AO⊥BO,所以ME∥AO,所以
t,又因为AO⊥BO,所以ME∥AO,所以![]() ,即
,即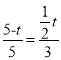 ,解得:t=
,解得:t=![]() ;
;

③如图:当BE=MN=t时,过点E作EF⊥BM于点F,所以BF=![]() BM=
BM=![]() (5-t),易证△BFE∽△BOA,所以
(5-t),易证△BFE∽△BOA,所以![]() ,即
,即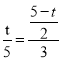 ,解得:t=
,解得:t=![]() .
.
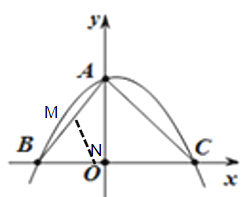
(3)设BP交y轴于点G,过点G作GH⊥AB于点H,因为BP恰好平分∠ABC,所以OG=GH,BH=BO=3,所以AH=2,AG=4-OG,在Rt△AHG中,由勾股定理得:OG=![]() ,设P(m,-
,设P(m,-![]() m2+
m2+![]() m+4),因为GO∥PD,∴△BGO∽△BPD,∴
m+4),因为GO∥PD,∴△BGO∽△BPD,∴![]() ,即
,即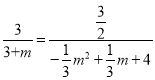 ,解得:m1=
,解得:m1=![]() ,m2=-3(点P在第一象限,所以不符合题意,舍去),m1=
,m2=-3(点P在第一象限,所以不符合题意,舍去),m1=![]() 时,-
时,-![]() m2+
m2+![]() m+4=
m+4=![]()
故点P的坐标为![]()