Question

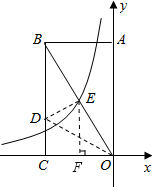
如图，矩形AOBC的两边OC、OA分别位于x轴、y轴上，点B的坐标为（-

5

，2

5

），D是CB边上的一点，将△CDO沿直线OD翻折，使C点恰好落在对角线OB上的点E处，若点E在一反比例函数的图象上，那么该函数的解析式是______．

Answer 1

作EF⊥CO于F．
∵点B的坐标为（-

5

，2

5

），
∴OB=

( 5 )2+(2 5 )2

=5，
∵OE=OC=

5

，
∴

EF

BC

=

EO

BO

，即

EF

2 5

=

5

5

，
∴EF=2．
在Rt△EFO中，
∵OF=

( 5 )2-22

=1，
∴E（-1，2），代入函数解析式y=

k

x

得，k=2×（-1）=-2，
∴函数解析式为y=-

2

x

．