Question

如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE=

1

4

BC=1．
（1）求证：CE=CF；
（2）若G在AD上，连接GC，且∠GCE=45°，求∠GCF的度数；
（3）在（2）的条件下，求GC的长度．

Answer 1

（1）证明：∵四边形ABCD是正方形，
∴BC=CD，∠BCD=∠B=∠ADC=∠CDF=90°，
在△EBC和△FDC中
∵

BE=DF ∠B=∠CDF BC=CD

，
∴△EBC≌△FDC（SAS），
∴CE=CF．

（2）∵△EBC≌△FDC，
∴∠BCE=∠DCF，
∵∠BCD=90°，∠GCE=45°，
∴∠BCE+∠GCD=90°-45°=45°，
∴∠GCD+∠DCF=45°，
∴∠GCF=45°．

（3）连接EG，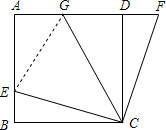
∠ECG=∠GCF=45°，
在△ECG和△FCG中
∵

EC=CF ∠ECG=∠FCG CG=CG

，
∴△ECG≌△FCG，
∴EG=GF，
∵DF=BE=

1

4

BC=1，
∴BC=CD=AD=AB=4，
设AG=x，则DG=4-x，GF=4-x+1=5-x=EG，AE=4-1=3，
在Rt△AEG中，由勾股定理得：3²+x²=（5-x）²，
解得：x=1.6，
DG=4-1.6=2.4，
在Rt△GCD中，由勾股定理得：GC=

42+2.42

=

4 34

5

．