题目内容
【题目】如图，在矩形ABCD中，M、N分别是边AD、BC的中点，点P、Q在DC边上，且PQ=
DC．若AB=16，BC=20，则图中阴影部分的面积是 ．
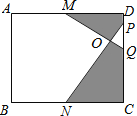
【答案】92
【解析】
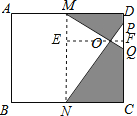
试题分析：连接MN，由于M，N分别是ADBC上的中点，所以MN∥AB∥CD，而四边形ABCD是长方形，所以四边形MNCD是矩形，再过O作OE⊥MN，同样也垂直于CD，再利用PQ=
DC，可得相似比，那么可求出OE，OF，以及MN，CD的长，再利用三角形的面积公式可求出△MNO和△PQO的面积，用矩形MNCD的面积减去△MNO的面积减去△PQO的面积，即可求阴影部分面积．
解：连接MN，过O作OE⊥MN，交MN于E，交CD于F，
在矩形ABCD中，AD∥BC，AD=BC，
∵M、N分别是边AD、BC的中点，
∴DM=CN，
∴四边形MNCD是平行四边形，
∴MN∥CD，
∴△OMN∽△PQO，
相似比是MN：PQ=4：1，
∴OE：OF=EF：GH=4：1，
又∵EF=
BC=10，
∴OE=8，OF=2，
∴S△MNO=×16×8=64，
∴S△PQO=×4×2=4，S矩形MNCD=16×10=160，
∴S阴影=160﹣64﹣4=92．
故答案为：92．
练习册系列答案
相关题目
