Question

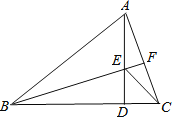
【题目】如图，△ABC中，∠C=90°，BC=6cm，AC=8cm，点P从点A开始沿AC向点C以2厘米/秒的速度运动；与此同时，点Q从点C开始沿CB边向点B以1厘米/秒的速度运动；如果P、Q分别从A、C同时出发，当其中一点到达终点时，另一点也随之停止运动．

（1）经过几秒，△CPQ的面积等于3cm2？

（2）在整个运动过程中，是否存在某一时刻t，使PQ恰好平分△ABC的面积？若存在，求出运动时间t；若不存在，请说明理由．

Answer 1

【答案】（1）x1=1，x2=3；（2）方程无实数根，即不存在满足条件的t．

【解析】

试题分析：（1）设出运动所求的时间，可将BP和BQ的长表示出来，代入三角形面积公式，列出等式，可将时间求出；

（2）将△PBQ的面积表示出来，根据△=b2﹣4ac来判断．

（1）解：设经过x秒，△CPQ的面积等于3cm2．则

x（8﹣2x）=3，

化简得x2﹣4x+3=0，

解得x1=1，x2=3；

（2）解：设存在某一时刻t，使PQ恰好平分△ABC的面积．则

t（8﹣2t）=××6×8，

化简得t2﹣4t+12=0，

b2﹣4ac=16﹣48=﹣32＜0，

故方程无实数根，即不存在满足条件的t．