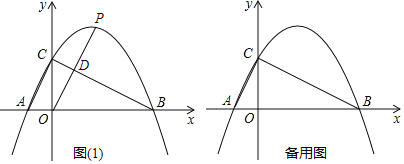题目内容
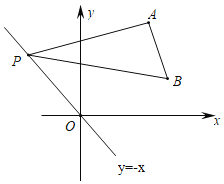
【题目】如图,在平面直角坐标系中,点A的坐标为(2![]() ,2
,2![]() ),点P在直线y=﹣x上运动,∠PAB=90°,∠APB=30°,在点P运动的过程中OB的最小值为( )
),点P在直线y=﹣x上运动,∠PAB=90°,∠APB=30°,在点P运动的过程中OB的最小值为( )
A.3.5B.2C.![]() D.2
D.2![]()
【答案】D
【解析】
如图中,作BH⊥OP于H,取PB的中点F,连接AF、FH、OA、AH.首先证明点B在射线HB上运动,推出当OB⊥BH时,OB的值最小,最小值为OH的长;
解:如图,作BH⊥OP于H,取PB的中点F,连接AF、FH、OA、AH.

在Rt△PAB和Rt△PBH中,
∵PF=FB,
∴AF=PF=FB=FH,
∴A、P、H、B四点共圆,
∵∠PAB=90°,∠APB=30°
∴![]()
∴∠AHB=∠APB=30°,∠AHP=∠ABP =60°,
∴点B在射线HB上运动,
∴当OB⊥BH时,OB的值最小,最小值为OH的长,
在Rt△AOH中,A(2![]() ,2
,2![]() )
)
∴OA=2![]() ,∠AHO=60°,
,∠AHO=60°,
∴OH=2![]() ,
,
∴OB的最小值为2![]() .
.
故选:D.

练习册系列答案
相关题目