题目内容
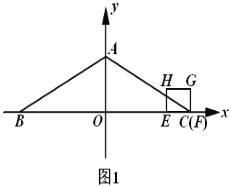
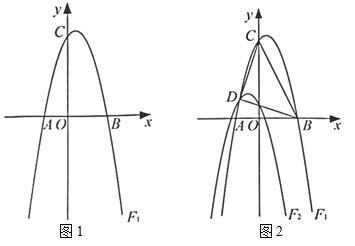
【题目】如图1所示,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
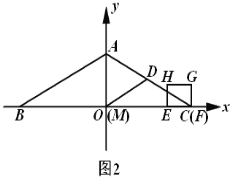
(2)如图2,将抛物线![]() 先向左平移1个单位,再向下平移3个单位,得到抛物线
先向左平移1个单位,再向下平移3个单位,得到抛物线![]() ,若抛物线
,若抛物线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①求点![]() 的坐标;
的坐标;
②判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)在(2)的条件下,抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①点
;(2)①点![]() 的坐标
的坐标![]() ;②
;②![]() 是等腰直角三角形,理由见解析;(3)
是等腰直角三角形,理由见解析;(3)![]() 或
或![]() .
.
【解析】
(1)将点![]() 代入即可得;
代入即可得;
(2)①先根据二次函数的平移规律得出抛物线![]() 的表达式,再联立两条抛物线的表达式求解即可得;
的表达式,再联立两条抛物线的表达式求解即可得;
②先根据抛物线![]() 的表达式求出点B、C的坐标,再利用两点之间的距离公式分别求出BC、BD、CD的长,然后根据勾股定理的逆定理、等腰三角形的定义即可得;
的表达式求出点B、C的坐标,再利用两点之间的距离公式分别求出BC、BD、CD的长,然后根据勾股定理的逆定理、等腰三角形的定义即可得;
(3)设点P的坐标为![]() ,根据等腰直角三角形的定义分三种情况:①当
,根据等腰直角三角形的定义分三种情况:①当![]() 时,先根据等腰直角三角形的性质、线段中点的点坐标求出点P的坐标,再代入抛物线
时,先根据等腰直角三角形的性质、线段中点的点坐标求出点P的坐标,再代入抛物线![]() 的表达式,检验点P是否在抛物线
的表达式,检验点P是否在抛物线![]() 的表达式上即可;②当
的表达式上即可;②当![]() 时,先根据平行四边形的判定得出四边形BCDP是平行四边形,再根据点C至点B的平移方式与点D至点P的平移方式相同可求出点P的坐标,然后代入抛物线
时,先根据平行四边形的判定得出四边形BCDP是平行四边形,再根据点C至点B的平移方式与点D至点P的平移方式相同可求出点P的坐标,然后代入抛物线![]() 的表达式,检验点P是否在抛物线
的表达式,检验点P是否在抛物线![]() 的表达式上即可;③当
的表达式上即可;③当![]() 时,先根据等腰直角三角形的性质得出点P在在线段BD的垂直平分线上,再利用待定系数法求出BD的垂直平分线上所在直线的解析式,然后根据两点之间的距离公式和
时,先根据等腰直角三角形的性质得出点P在在线段BD的垂直平分线上,再利用待定系数法求出BD的垂直平分线上所在直线的解析式,然后根据两点之间的距离公式和![]() 可求出点P的坐标,最后代入抛物线
可求出点P的坐标,最后代入抛物线![]() 的表达式,检验点P是否在抛物线
的表达式,检验点P是否在抛物线![]() 的表达式上即可.
的表达式上即可.
(1)将点![]() 代入抛物线
代入抛物线![]() 的表达式得:
的表达式得:![]()
解得![]()
则抛物线![]() 的表达式为
的表达式为![]()
故抛物线![]() 的表达式为
的表达式为![]() ;
;
(2)①由二次函数的平移规律得:抛物线![]() 的表达式为
的表达式为![]()
即![]()
联立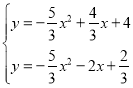 ,解得
,解得![]()
则点![]() 的坐标为
的坐标为![]() ;
;
②对于![]()
当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]()
则点B的坐标为![]()
当![]() 时,
时,![]() ,则点C的坐标为
,则点C的坐标为![]()
由两点之间的距离公式得:![]()
![]()
![]()
则![]() ,
,![]()
故![]() 是等腰直角三角形;
是等腰直角三角形;
(3)抛物线![]() 的表达式为
的表达式为![]()
设点P的坐标为![]()
由题意,分以下三种情况:
①当![]() 时,
时,![]() 为等腰直角三角形
为等腰直角三角形
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]()
![]()
![]()
![]() 点D是CP的中点
点D是CP的中点
则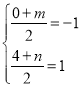 ,解得
,解得![]()
即点P的坐标为![]()
对于抛物线![]() 的表达式
的表达式![]()
当![]() 时,
时,![]()
即点![]() 在抛物线
在抛物线![]() 上,符合题意
上,符合题意
②当![]() 时,
时,![]() 为等腰直角三角形
为等腰直角三角形
![]() ,
,![]()
![]() ,
,![]()
![]() 四边形BCDP是平行四边形
四边形BCDP是平行四边形
![]() 点C至点B的平移方式与点D至点P的平移方式相同
点C至点B的平移方式与点D至点P的平移方式相同
![]()
![]() 点C至点B的平移方式为先向下平移4个单位长度,再向右平移2个单位长度
点C至点B的平移方式为先向下平移4个单位长度,再向右平移2个单位长度
![]()
![]()
即点P的坐标为![]()
对于抛物线![]() 的表达式
的表达式![]()
当![]() 时,
时,![]()
即点![]() 在抛物线
在抛物线![]() 上,符合题意
上,符合题意
③当![]() 时,
时,![]() 为等腰直角三角形
为等腰直角三角形
则点P在线段BD的垂直平分线上
设直线BD的解析式![]()
将点![]() 代入得:
代入得:![]() ,解得
,解得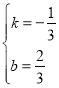
则直线BD的解析式![]()
设BD的垂线平分线所在直线的解析式为![]()
点![]() 的中点的坐标为
的中点的坐标为![]() ,即
,即![]()
将点![]() 代入
代入![]() 得:
得:![]() ,解得
,解得![]()
则BD的垂线平分线所在直线的解析式为![]()
因此有![]() ,即点P的坐标为
,即点P的坐标为![]()
由两点之间的距离公式得:![]()
又![]() ,
,![]() 为等腰直角三角形
为等腰直角三角形
![]()
则![]()
解得![]() 或
或![]()
当![]() 时,
时,![]() ,即点P的坐标为
,即点P的坐标为![]()
当![]() 时,
时,![]() ,即点P的坐标为
,即点P的坐标为![]()
对于抛物线![]() 的表达式
的表达式![]()
当![]() 时,
时,![]()
即点![]() 不在抛物线
不在抛物线![]() 上,不符合题意,舍去
上,不符合题意,舍去
当![]() 时,
时,![]()
即点![]() 不在抛物线
不在抛物线![]() 上,不符合题意,舍去
上,不符合题意,舍去
综上,符合条件的点P的坐标为![]() 或
或![]() .
.

【题目】2020年2月,贵州省积极响应国家“停课不停学”的号召,推出了“空中黔课”.为了解某中学初三学生每天听空中黔课的时间,随机调查了该校部分初三学生.根据调查结果,绘制出了如下统计图表(不完整),请根据相关信息,解答下列问题:
部分初三学生每天听空中黔课时间的人数统计表
时间/ | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
人数/人 | 2 | 6 | 6 | 10 |
| 4 |
部分初三学生每天听空中黔课时间的人数统计图
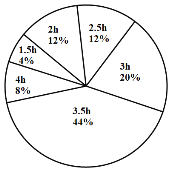
(1)本次共调查的学生人数为_____,在表格中,![]() ___;
___;
(2)统计的这组数据中,每天听空中黔课时间的中位数是____,众数是_____;
(3)请就疫情期间如何学习的问题写出一条你的看法.
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8