题目内容
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

【答案】(1)45°;(2)45°;(3) ∠DOE的大小发生变化.45°或135°.
【解析】试题分析:
(1)因为∠DOE=∠COD+∠COE,所以分别根据角平分线的定义求出∠COD和∠COE即可;
(2)因为∠DOE=∠COD+∠COE,结合角平分线即可求解;
(3)需要分类,当∠AOC是钝角时和当∠AOC大于钝角时,结合角平分线求解.
试题解析:
(1) 根据题意得∠AOC=90°-∠BOC=20°.因为OD,OE分别平分∠AOC和∠BOC,所以∠COD=![]() ∠AOC=10°,∠COE=
∠AOC=10°,∠COE=![]() ∠BOC=35°,所以∠DOE=∠COD+∠COE=45°
∠BOC=35°,所以∠DOE=∠COD+∠COE=45°
(2) ∠DOE的大小不变,理由:∠DOE=∠COD+∠COE=![]() ∠AOC+
∠AOC+![]() ∠COB=
∠COB=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)= ![]() ∠AOB=45°
∠AOB=45°
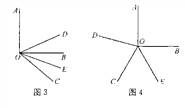
(3) ∠DOE的大小发生变化.如图3,则∠DOE为45°;如图4,则∠DOE为135°

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
摸到白球的频率 | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(1)按表格数据格式,表中的a=;b=;
(2)请估计:当次数s很大时,摸到白球的频率将会接近;
(3)请推算:摸到红球的概率是(精确到0.1);
(4)试估算:口袋中红球有多少只?
(5)解决了上面4个问题后,请你从统计与概率方面谈一条启示.

