Question

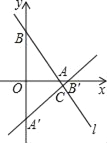
【题目】如图，在平面直角坐标系中，直线y＝﹣2x+4分别交x轴、y轴于点A、B，将△AOB绕点O顺时针旋转90°后得到△A′OB′．

（1）求直线A′B′所对应的函数表达式．

（2）若直线A′B′与直线AB相交于点C，求△A′BC的面积．

Answer 1

【答案】（1）y=（2）

【解析】

（1）先根据一次函数的解析式求出AB两点的坐标，再由图形旋转的性质求出的坐标，用待定系数法求出直线的解析式即可。

（2）直接根据三角形的坐标，利用三角形的面积公式进行计算即可。

（1）∵直线y＝﹣2x+4分别交x轴、y轴于点A、B，

∴点A、B的坐标分别为（2，0）、（0，4）．

由旋转得，点A′、B′的坐标分别为（0，﹣2）、（4，0）．

设直线A′B′所对应的函数表达式为y＝kx+b．

∴

解得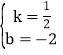

∴直线A′B′所对应的函数表达式为y=x-2

（2）依题意有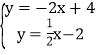

解得

∴点C的横坐标为

∵A′B＝4﹣（﹣2）＝6，

∴S△A′BC=A′Bx=