题目内容
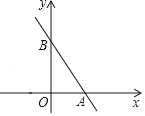
【题目】如图,直线l的解析式为y=﹣![]() x+b,它与坐标轴分别交于A、B两点,其中点B坐标为(0,4).
x+b,它与坐标轴分别交于A、B两点,其中点B坐标为(0,4).
(1)求出A点的坐标;
(2)在第一象限的角平分线上是否存在点Q使得∠QBA=90°?若存在,求点Q的坐标;若不存在,请说明理由.
(3)动点C从y轴上的点(0,10)出发,以每秒1cm的速度向负半轴运动,求出点C运动所有的时间t,使得△ABC为轴对称图形(直接写答案即可)
【答案】(1)A(3,0);(2)存在.Q(16,16);(3)当C点运动1秒、![]() 秒、11秒、14秒时,能使△ABC为轴对称图形.
秒、11秒、14秒时,能使△ABC为轴对称图形.
【解析】
(1)利用点B代入直线,求出直线解析式,然后求直线与x轴交点坐标;
(2)点Q在第一象限角平分线上,设Q(x,x),已知给出了指定角,利用勾股定理列方程,即可求出点Q的标;
(3)求△ABC为轴对称图形,实质是求动点C,使△ABC为等腰三角形,根据等腰三角形性质分类讨论即可求出点的坐标,利用点的坐标求出运动时间.
(1)将点B(0,4)代入直线l的解析式得:
b=4,
∴直线l的解析式为:y=﹣![]() x+4,
x+4,
令y=0得:x=3,
∴A(3,0).
(2)存在.
∵Q在第一象限的角平分线上,
设Q(x,x),
根据勾股定理:
QB2+BA2=QA2,
x2+(x﹣4)2+52=x2+(x﹣3)2,
解得x=16,
故Q(16,16).
(3)能使△ABC为轴对称图形,
则得:△ABC为等腰三角形,
当AB=BC时,
C(0,9)或(0,﹣1),
此时C点运动1秒或11秒,
当AB=AC时,
C(0,﹣4),
此时C点运动14秒,
当AC=BC时,
C(0,![]() ),
),
此时C点运动![]() 秒.
秒.
综上所述:当C点运动1秒、![]() 秒、11秒、14秒时,能使△ABC为轴对称图形.
秒、11秒、14秒时,能使△ABC为轴对称图形.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】某市开展了“雷锋精神你我传承,关爱老人从我做起”的主题活动,随机调查了本市部分老人与子女同住情况,根据收集到的数据,绘制成如下统计图表(不完整) 老人与子女同住情况百分比统计表
老人与子女 | 同住 | 不同住 | 不同住 | 其他 |
A | 50% | B | 5% |
根据统计图表中的信息,解答下列问题: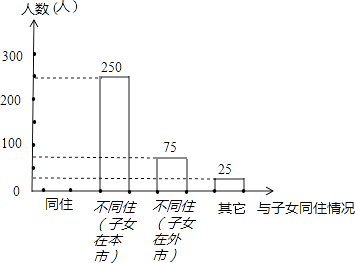
(1)求本次调查的老人的总数及a、b的值;
(2)将条形统计图补充完整;(画在答卷相对应的图上)
(3)若该市共有老人约15万人,请估计该市与子女“同住”的老人总数.