题目内容
【题目】某校为了解学生最喜欢的球类运动情况,随机选取该校部分学生进行调查,要求每名学生只写一类最喜欢的球类运动,以下是根据调查结果绘制的统计图的一部分,
类别 |
|
|
|
|
|
|
类型 | 足球 | 羽毛球 | 乒乓球 | 篮球 | 排球 | 其它 |
人数 |
|
|
|
|

根据以上信息,解答下列问题:
(1)被调查学生的总人数为 人.
(2)最喜欢篮球的有 人,最喜欢足球的学生数占被调查总人数的百分比为 %
(3)该校共有![]() 名学生,根据调查结果,估计该校最喜欢排球的学生人数有多少?
名学生,根据调查结果,估计该校最喜欢排球的学生人数有多少?
【答案】(1)50;(2)16,24;(3)180.
【解析】
(1)由喜欢羽毛球的人数10去除以它在扇形统计图中占的百分比(20%)即可求得总人数;
(2)由(1)题中求得的总人数乘以D项在扇形统计图中所占百分比可得最喜欢篮球的人数;先求出最喜欢足球的人数,再除以总人数即得最喜欢足球的学生数占被调查总人数的百分比;
(3)利用样本估计总体的方法,即可求得答案.
解:(1)10÷20%=50,所以被调查学生的总人数为50人;
故答案为50;
(2)最喜欢篮球的人数为50×32%=16,
最喜欢足球的学生数=50-10-4-16-6-2=12,
占被调查总人数的百分比为12÷50=24%;
故答案为16,24;
(3)![]() .
.
答:该校最喜欢排球的学生人数大约有180人.

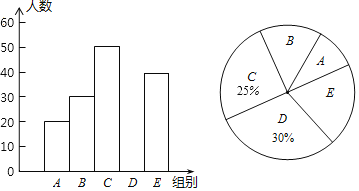
【题目】某校七年级举行“数学计算能力”比赛,比赛结束后,随机抽查部分学生的成绩,根据抽查结果绘制成如下的统计图表
组别 | 分数x | 频数 |
A | 40≤x<50 | 20 |
B | 50≤x<60 | 30 |
C | 60≤x<70 | 50 |
D | 70≤x<80 | m |
E | 80≤x<90 | 40 |
根据以上信息解答下列问题:
(1)共抽查了 名学生,统计图表中,m= ,请补全直方图;
(2)求扇形统计图中“B组”所对应的圆心角的度数;
(3)若七年级共有800名学生,分数不低于60分为合格,请你估算本次比赛全年级合
格学生的人数
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)