题目内容
【题目】如图1，△ABC中，CD⊥AB于D，且BD : AD : CD＝2 : 3 : 4，
（1）试说明△ABC是等腰三角形；
（2）已知S△ABC＝40cm2，如图2，动点M从点B出发以每秒2cm的速度沿线段BA向点A 运动，同时动点N从点A出发以每秒1cm速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止. 设点M运动的时间为t（秒），
①若△DMN的边与BC平行，求t的值；
②若点E是边AC的中点，问在点M运动的过程中，△MDE能否成为等腰三角形？若能，求出t的值；若不能，请说明理由．
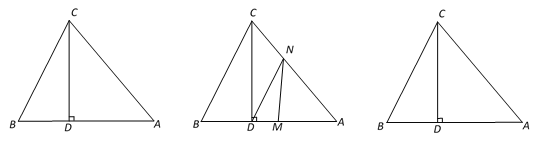
图1 图2 备用图
【答案】（1）见详解；（2）①t值为：
s或6s；②t值为：4.5或5或
．
【解析】
（1）设BD=2x，AD=3x，CD=4x，则AB=5x，由勾股定理求出AC，即可得出结论；
（2）由△ABC的面积求出BD、AD、CD、AC；①当MN∥BC时，AM=AN；当DN∥BC时，AD=AN；得出方程，解方程即可；
②根据题意得出当点M在DA上，即2＜t≤5时，△MDE为等腰三角形，有3种可能：如果DE=DM；如果ED=EM；如果MD=ME=2t-4；分别得出方程，解方程即可．
解：（1）证明：设BD=2x，AD=3x，CD=4x，则AB=5x，
在Rt△ACD中，AC=5x，
∴AB=AC，
∴△ABC是等腰三角形；
（2）解：由（1）知，AB=5x，CD=4x，
∴S△ABC=
×5x×4x=40cm2，而x＞0，
∴x=2cm，
则BD=4cm，AD=6cm，CD=8cm，AB=AC=10cm．
由运动知，AM=10-2t，AN=t，
①当MN∥BC时，AM=AN，
即10-2t=t，
∴
；
当DN∥BC时，AD=AN，
∴6=t，
得：t=6；
∴若△DMN的边与BC平行时，t值为s或6s．
②存在，理由：
Ⅰ、当点M在BD上，即0≤t＜2时，△MDE为钝角三角形，但DM≠DE；
Ⅱ、当t=2时，点M运动到点D，不构成三角形
Ⅲ、当点M在DA上，即2＜t≤5时，△MDE为等腰三角形，有3种可能．
∵点E是边AC的中点，
∴DE=AC=5
当DE=DM，则2t-4=5，
∴t=4.5s；
当ED=EM，则点M运动到点A，
∴t=5s；
当MD=ME=2t-4，
如图，过点E作EF垂直AB于F，
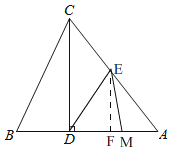
∵ED=EA，
∴DF=AF=AD=3，
在Rt△AEF中，EF=4；
∵BM=2t，BF=BD+DF=4+3=7，
∴FM=2t-7
在Rt△EFM中，（2t-4）2-（2t-7）2=42，
∴t=．
综上所述，符合要求的t值为4.5或5或．
