题目内容
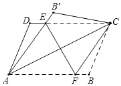
【题目】在△ABC中,点A到直线BC的距离为d,AB>AC>d,以A为圆心,AC为半径画圆弧,圆弧交直线BC于点D,过点D作DE∥AC交直线AB于点E,若BC=4,DE=1,∠EDA=∠ACD,则AD=__________.
【答案】2或-2+2![]()
【解析】
当∠ACB为锐角时,根据题意易证∠BDE=∠ADE=∠ADC=∠ACD=60°,则△ACD为等边三角形,设AD=x,根据△BDE∽△BCA,列出关于x的方程,然后求解方程即可,同理求出当∠ACB为钝角时,AD的长即可.
解:如图,当∠C为锐角时,
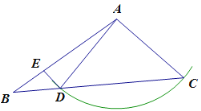
∵AD=AC,
∴∠ADC=∠ACD,
∵DE∥AC,
∴∠BDE=∠ACD,
已知∠EDA=∠ACD,
∴∠BDE=∠ADE=∠ADC=∠ACD=60°,
∴△ACD为等边三角形,
∵DE∥AC,
∴△BDE∽△BCA,
设AD=AC=CD=x,
则![]() ,即
,即![]() ,
,
解得x=2,
∴AD=2;
如图,当∠ACB为钝角时,
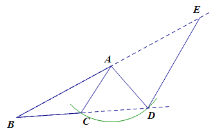
同理可得△ACD为等边三角形,
∵DE∥AC,
∴△BCA∽△BDE,
设AD=AC=CD=x,
则![]() ,即
,即![]() ,
,
解得x=﹣2+2![]() ,
,
∴AD=﹣2+2![]() .
.
故答案为:2或-2+2![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目