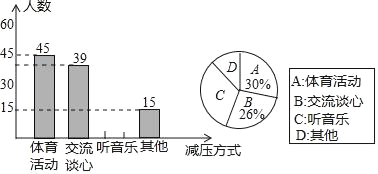
��Ŀ����
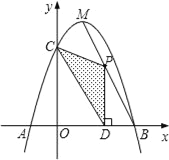
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��y���ϣ�������Ϊ��0��4����x���ϵ�һ��
P��ԭ��O��������x�������᷽���˶����ٶ�Ϊÿ��1����λ���ȣ���PΪֱ�Ƕ���
��һ������������Rt��APB����P����˶�ʱ��Ϊt�룮

��1����գ���t��2ʱ����B������Ϊ��
��2����P����˶������У���AB��x��ʱ����t��ֵ��
��3��ͨ��̽������������P���˶����δ�����Bʼ����һֱ���ϣ��������ֱ�ߵĺ�������ʽ��
���𰸡���1������2��4������2��t=4����3��y��x��4
��������
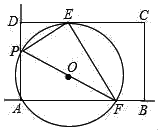
��1������P����������ƽ��2����λ�����O����ʱ����A������Ϊ������2��4��������AΧ�Ƶ�O˳ʱ����ת90������ʱ��B������Ϊ����4��2��������B����������ƽ��2����λ����Ϊ��ʱ�ĵ�B��6��2����������⣻
��2������B��BC��x���ڵ�C����ͼ��ʾ��֤���ı���ABCOΪ�����Σ���AO��BC��4�����APBΪ����ֱ�������Σ�������⣻
��3��֤����PAO�ա�BPC��AAS������AP��BP��AO��PC��BC��PO����A��0��4������P��t��0������B��x��y������PC��AO��4��BC��PO��t��y��CO��PC+PO��4+y��x��������⣮
��1������P����������ƽ��2����λ�����O����ʱ����A������Ϊ������2��4����
����AΧ�Ƶ�O˳ʱ����ת90������ʱ��B������Ϊ����4��2����
����B����������ƽ��2����λ����Ϊ��ʱ�ĵ�B��6��2����
��2������B��BC��x���ڵ�C����ͼ��ʾ��

��AO��x�ᣬBC��x�ᣬ��AB��x�ᣬ
���ı���ABCOΪ�����Σ�
��AO��BC��4��
�ߡ�APBΪ����ֱ�������Σ�
��AP��BP����PAB����PBA��45����
���OAP��90������PAB��45����
���AOPΪ����ֱ�������Σ�
��OA��OP��4��t��4��1��4���룩��
��3���ߡ�APBΪ����ֱ�������Σ�
���APO+��BPC��180����90����90����
�֡ߡ�PAO+��APO��90�������PAO����BPC��
��PAO����BPC��
�ڡ�PAO�͡�BPC�У���AOP����PCB��90����
���PAO�ա�BPC��AAS����
AP��BP��
��AO��PC��BC��PO��
�ߵ�A��0��4������P��t��0������B��x��y����
��PC��AO��4��BC��PO��t��y��CO��PC+PO��4+y��x��
��y��x��4��

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�����Ŀ������ɽ���������мס��������ǹ�����kg�������ǹ����ۼۺͽ������
�ǹ� | ���� | ���� |
�ۼ� | 36Ԫ/kg | 20Ԫ/kg |
���� | 30Ԫ/kg | 16Ԫ/kg |
��1���������üס��������ǹ���ϳ��Ӱ��dz��ۣ���Ϻ��ǹ����ۼ���27.2Ԫ/kg����Ҫ���������Ӱ��ǹ�100/kg����Ҫ�ס��������ǹ�������ǧ�ˣ�
��2������һ����ͯ��ǰϦ����������5000Ԫ�����ס��������ǹ���200kg����ν�������ʹ�����ǹ�������������������Ƕ��٣���ע��������ֻ��Ϊ������