题目内容
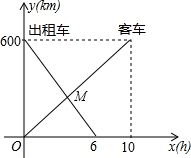一辆客车从甲地开往乙地，一辆出租车从地开往甲地，两车同时出发，客车离甲地的距离为y1（km），出租车离甲地的距离为y2（km），客车行驶时间为x（h），y1，y2与x的函数关系图象如图12所示：（1）根据图象，求出y1y2，关于x的函数关系式．
（2）若设两车间的距离为（km），请写出S关于x的函数关系式．
分析：（1）设y1=k1x，y2=k2x+b，根据图形由待定系数法求出其解即可；
（2）先由（1）的解析式求出相遇的时间，再根据时间分两种情况由行程问题的数量关系就可以得出解析式．
（2）先由（1）的解析式求出相遇的时间，再根据时间分两种情况由行程问题的数量关系就可以得出解析式．
解答：解：（1）设设y1=k1x，y2=k2x+b，由题意，得
600=10k1，
k1=60，
∴y1=60x；
，
解得：
，
∴y2=-100x+600
（2）由题意，得
60x=-100x+600，
解得：x=
．
由函数图象可以求出客车的速度为：600÷10=60km/h，
出租车的速度为：600÷6=100km/h．
当0≤x≤
时
S1=600-60x-100x=600-160x．
当
＜x≤6时，
S2=160x-600
当6＜x≤10时，
S3=60x．
∴S=
．
600=10k1，
k1=60，
∴y1=60x；
|
解得：
|
∴y2=-100x+600
（2）由题意，得
60x=-100x+600，
解得：x=
| 15 |
| 4 |
由函数图象可以求出客车的速度为：600÷10=60km/h，
出租车的速度为：600÷6=100km/h．
当0≤x≤
| 15 |
| 4 |
S1=600-60x-100x=600-160x．
当
| 15 |
| 4 |
S2=160x-600
当6＜x≤10时，
S3=60x．
∴S=
|
点评：本题考查了待定系数法求一次函数的解析式的运用，一元一次方程的解法的运用，分类讨论思想的运用，行程问题的数量关系的运用，解答时求出一次函数的解析式是关键，分类讨论是难点．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
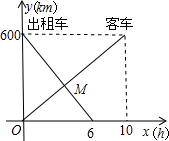距离为y1（km），出租车离甲地的距离为y2（km），客车行驶时间为x（h），y1，y2与x的函数关系图象如图所示：
（2013•黄石）一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为y1千米，出租车离甲地的距离为y2千米，两车行驶的时间为x小时，y1、y2关于x的函数图象如图所示：
一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，在行驶过程中，设客车离甲地的距离为y1千米，出租车离甲地的距离为y2千米，两地行驶的时间为x小时，y1、y2关于x的函数图象如图所示：