题目内容
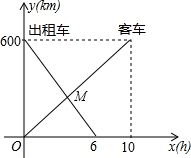 (2013•婺城区一模)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:
(2013•婺城区一模)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:(1)根据图象,直接写出y1,y2关于x的函数关系式:y1=
60x
60x
,y2=-100x+600
-100x+600
;(2)甲、乙两地间有A、B两个加油站,相距280km,若客车进入A站加油时,出租车恰好进入B站加油.求A加油站到甲地的距离.
分析:(1)利用待定系数法求一次函数解析式解答即可;
(2)分A加油站在甲地与B加油站之间,B加油站在甲地与A加油站之间两种情况列出方程求解即可.
(2)分A加油站在甲地与B加油站之间,B加油站在甲地与A加油站之间两种情况列出方程求解即可.
解答:解:(1)设y1=k1x,
由图可知,函数图象经过点(10,600),
所以10k1=600,
解得k1=60,
所以,y1=60x(0≤x≤10),
设y2=k2x+b,
由图可知,函数图象经过点(0,600),(6,0),
则
,
解得
,
所以,y2=-100x+600(0≤x≤6);
(2)设两车距离为S,
①A加油站在甲地与B加油站之间时,(-100x+600)-60x=280,
解得x=2,
此时,A加油站距离甲地:60×2=120km,
②B加油站在甲地与A加油站之间时,60x-(-100x+600)=280,
解得x=
,
此时,A加油站距离甲地:60×
=330km,
综上所述,A加油站到甲地距离为120km或330km.
由图可知,函数图象经过点(10,600),
所以10k1=600,
解得k1=60,
所以,y1=60x(0≤x≤10),
设y2=k2x+b,
由图可知,函数图象经过点(0,600),(6,0),
则
|
解得
|
所以,y2=-100x+600(0≤x≤6);
(2)设两车距离为S,
①A加油站在甲地与B加油站之间时,(-100x+600)-60x=280,
解得x=2,
此时,A加油站距离甲地:60×2=120km,
②B加油站在甲地与A加油站之间时,60x-(-100x+600)=280,
解得x=
| 11 |
| 2 |
此时,A加油站距离甲地:60×
| 11 |
| 2 |
综上所述,A加油站到甲地距离为120km或330km.
点评:本题考查了一次函数的应用,主要根据待定系数法求一次函数解析式,根据图象准确获取信息是解题的关键,(2)注意要分情况讨论.

练习册系列答案
相关题目
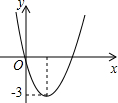 (2013•婺城区一模)如图是二次函数y=ax2+bx的图象,若一元二次方程ax2+bx+m=0有实数根,则实数m的最大值为
(2013•婺城区一模)如图是二次函数y=ax2+bx的图象,若一元二次方程ax2+bx+m=0有实数根,则实数m的最大值为 (2013•婺城区一模)热气球C从建筑物A的底部沿直线开始斜着往上飞行,当飞行了180米距离时到达如图中的位置,此时在热气球上测得两建筑物A,B底部的俯角分别为30°和60°﹒若此时热气球在地面的正投影D与点A,B在同一直线上﹒
(2013•婺城区一模)热气球C从建筑物A的底部沿直线开始斜着往上飞行,当飞行了180米距离时到达如图中的位置,此时在热气球上测得两建筑物A,B底部的俯角分别为30°和60°﹒若此时热气球在地面的正投影D与点A,B在同一直线上﹒