题目内容
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:

(1)根据图象,填空:客车的速度是
(2)写出y1,y2关于x的函数关系式;
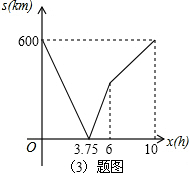
(3)若设两车间的距离为s(km),求s关于x的函数关系式;并在备用图中画出它的函数图象;
(4)甲、乙两地间有A,B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油.求A加油站到甲地的距离.

(1)根据图象,填空:客车的速度是
60
60
km/h,出租车的速度是100
100
km/h;(2)写出y1,y2关于x的函数关系式;
(3)若设两车间的距离为s(km),求s关于x的函数关系式;并在备用图中画出它的函数图象;
(4)甲、乙两地间有A,B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油.求A加油站到甲地的距离.
分析:(1)根据速度=路程÷时间,列式进行计算即可得解;
(2)根据两函数图象经过的点的坐标,利用待定系数法求一次函数解析式解答即可;
(3)先求出出租车与客车相遇的时间为
小时,然后分①0≤x<
时,两车的距离为两地间的距离减去两车行驶的路程;②
≤x<6时,两车的距离为两车行驶的路程减去两地间的距离;③6≤x≤10时,两车间的距离为客车行驶的路程;然后利用两点法作一次函数图象作出函数图象即可;
(4)由(3)的函数关系式,根据A、B两个加油站相距200米列出方程求解得到进站加油的时间,然后根据客车行驶的路程求出A加油站到甲地的距离.
(2)根据两函数图象经过的点的坐标,利用待定系数法求一次函数解析式解答即可;
(3)先求出出租车与客车相遇的时间为
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
(4)由(3)的函数关系式,根据A、B两个加油站相距200米列出方程求解得到进站加油的时间,然后根据客车行驶的路程求出A加油站到甲地的距离.
解答:解:(1)由图可知,甲乙两地间的距离为600km,
所以,客车速度=
=60km/h,
出租车速度=
=100km/h;
故答案为:60,100;
(2)设客车的函数关系式为y1=k1x,则10k1=600,
解得k1=60,
所以,y1=60x(0≤x≤10),
设出租车的函数关系式为y2=k2x+b,
则
,
解得
,
所以,y2=-100x+600(0≤x≤6);
(3)当出租车与客车相遇时,60x+100x=600,
解得x=
,
①0≤x<
时,S=600-(60+100)x=-160x+600,
②
≤x<6时,S=(60+100)x-600=160x-600,
③6≤x≤10时,S=60x,
所以,s关于x的函数关系式为:S=
;
画图正确;
(4)由题意得:S=200,①当0≤x<
时,-160x+600=200,
解得x=
,
所以,y1=60x=150km;
②当
≤x<6时,160x-600=200,
解得x=5,
所以,y1=300km;
③当6≤x≤10时,60x≥360>200(不合题意),
因此,A加油站到甲地距离为150km或300km.
所以,客车速度=
| 600 |
| 10 |
出租车速度=
| 600 |
| 6 |
故答案为:60,100;
(2)设客车的函数关系式为y1=k1x,则10k1=600,
解得k1=60,
所以,y1=60x(0≤x≤10),
设出租车的函数关系式为y2=k2x+b,
则
|
解得
|
所以,y2=-100x+600(0≤x≤6);
(3)当出租车与客车相遇时,60x+100x=600,
解得x=
| 15 |
| 4 |

①0≤x<
| 15 |
| 4 |
②
| 15 |
| 4 |
③6≤x≤10时,S=60x,
所以,s关于x的函数关系式为:S=
|
画图正确;
(4)由题意得:S=200,①当0≤x<
| 15 |
| 4 |
解得x=
| 5 |
| 2 |
所以,y1=60x=150km;
②当
| 15 |
| 4 |
解得x=5,
所以,y1=300km;
③当6≤x≤10时,60x≥360>200(不合题意),
因此,A加油站到甲地距离为150km或300km.
点评:本题考查了一次函数的应用,主要利用了相遇问题,相背问题的关系,读懂题意,看到图形,理清两车的运行关系与两车之间的距离的变化情况是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
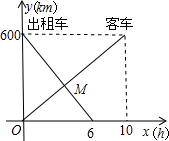 距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:
距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示: (2013•黄石)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示:
(2013•黄石)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示: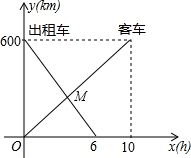 (2013•婺城区一模)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:
(2013•婺城区一模)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示: 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,在行驶过程中,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两地行驶的时间为x小时,y1、y2关于x的函数图象如图所示:
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,在行驶过程中,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两地行驶的时间为x小时,y1、y2关于x的函数图象如图所示: