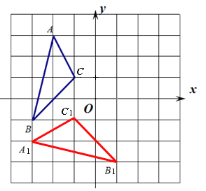
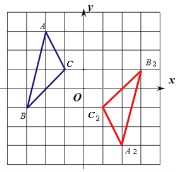
��Ŀ����
����Ŀ�����Ķ������������ǹ���������������Ҫ����������ʮһ��ѧУ�ԡ����Ķ�����ɫ�γ�ʵʩΪͻ�ƿڣ���������ѧ���ĺ�����������ȫУʦ��������Ӧ����ϣ���չ���ֻ�ḻ������������ѧ��ȤС���У�ͬѧ�Ǵ�������ʶ�˺ܶ���Ȥ������������һ������ƽ����������ͬѧ�ǵ���Ȥ���������£�һ����λ������ǧλ�ϺͰ�λ�ϵ�����֮��Ϊx��ʮλ�Ϻ�λ�ϵ�����֮��Ϊy�����![]() ����ô�������λ��Ϊ����ƽ������
����ô�������λ��Ϊ����ƽ������
���磺1423��![]() ��
��![]() ����Ϊ
����Ϊ![]() ������1423�ǡ���ƽ������
������1423�ǡ���ƽ������
��1��ֱ��д������С�ġ���ƽ������________�����ġ���ƽ������__________��
��2����ͬʱ�����������������С���ƽ������
�ٸ�λ�ϵ�������ǧλ�ϵ����ֵ�������
�ڰ�λ�ϵ�������ʮλ�ϵ�����֮����12�ı�����
��3����һ������ƽ�����ĸ�λ����ʮλ�ϵ����ֽ���λ�ã�ͬʱ������λ����ǧλ�ϵ����ֽ���λ�ã��ƽ���ǰ������������ƽ����Ϊ����غ�ƽ������
���磺1423��4132Ϊ����غ�ƽ����
��֤���������������غ�ƽ����֮����1111�ı�����
���𰸡���1��1001��9999����2��2754��4848����3��������
��������
��1�����ݡ���ƽ�����Ķ����ֱ�ӵó���С�ġ���ƽ������1001�����ġ���ƽ������9999��
��2�����������ƽ������ǧλ������a����λ������m��ʮλ������n������a��m��n������������![]() ��
��![]() ��
��![]() ����������2a������
�����λ������2a������![]() �õ�a�Ŀ���ȡֵΪ1��2��3��4�����ݰ�λ�ϵ�������ʮλ�ϵ�����֮����12�ı�������֪m+n=12���õ�
�õ�a�Ŀ���ȡֵΪ1��2��3��4�����ݰ�λ�ϵ�������ʮλ�ϵ�����֮����12�ı�������֪m+n=12���õ�![]() ����a�Ŀ���ȡֵ�ɵ�m��ȡֵ��������÷��������ġ���ƽ������
����a�Ŀ���ȡֵ�ɵ�m��ȡֵ��������÷��������ġ���ƽ������
��3��������һ������ƽ����ǧλ����Ϊa����λ����Ϊb��ʮλ����Ϊc����λ����Ϊd�������ġ���غ�ƽ����ǧλ����Ϊb����λ����Ϊa��ʮλ����Ϊd����λ����Ϊc���������ǵĺͣ����ݡ���ƽ�����Ķ����֪a+b=c+d����ʽ�ֽ�ɵ�ԭʽ= 1111(a+b)������֤����
�⣺��1�����ݡ���ƽ�����Ķ���ɵã�
��С�ġ���ƽ����1001�����ġ���ƽ����9999��
�ʴ�Ϊ1001��9999��
��2�����������ƽ������ǧλ������a����λ������m��ʮλ������n������a��m��n������������![]() ��
��![]() ��
��![]() ��
��
��������2a��
�֡�![]() ��
��
��a�Ŀ���ȡֵΪ1��2��3��4��
�߰�λ�ϵ�������ʮλ�ϵ�����֮����12�ı�����
��m+n=0��m+n=12��
�ߡ���ƽ������a+m=n+2a��
��m+n=0ʱ����m=n=0�����ʱa=0�����������⣬
��m+n=12��
��a+m=12m+2a����ã�![]() ��
��
��a�Ŀ���ȡֵΪ1��2��3��4����mΪ��������
��m�Ŀ���ȡֵΪ7��8��
��a=2ʱ��m=7���������ƽ������2754��
��a=4ʱ��m=8���������ƽ������4848��
�������������������ġ���ƽ������2754��4848��
��3��������һ������ƽ����ǧλ����Ϊa����λ����Ϊb��ʮλ����Ϊc����λ����Ϊd�������ġ���غ�ƽ����ǧλ����Ϊb����λ����Ϊa��ʮλ����Ϊd����λ����Ϊc��
��![]()
![]()
![]()
�ɡ���ƽ�����Ķ����֪��a+b=c+d��
��ԭʽ![]()
![]() ��
��
��a��bΪ����������![]() �ܱ�1111������
�ܱ�1111������
��![]() �ܱ�1111������
�ܱ�1111������
���������������غ�ƽ����֮����1111�ı�����

 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д�����Ŀ��Ϊ�˼�ǿ��У����İ�ȫ��أ�����ƽ��У��ijѧУ�ƻ�����![]() ̨��������豸�����мס��������ͺŵ��豸������ÿ̨�۸���Ч��ذ뾶�����ʾ�������飬����
̨��������豸�����мס��������ͺŵ��豸������ÿ̨�۸���Ч��ذ뾶�����ʾ�������飬����![]() ̨�����豸�ȹ���
̨�����豸�ȹ���![]() ̨�����豸��
̨�����豸��![]() Ԫ������
Ԫ������![]() ̨�����豸�ȹ���
̨�����豸�ȹ���![]() ̨�����豸��
̨�����豸��![]() Ԫ.
Ԫ.
���� | ���� | |
�۸�Ԫ/̨�� |
|
|
��Ч�뾶����/̨�� |
|
|
��![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
��![]() ������������豸���ʽ���
������������豸���ʽ���![]() Ԫ���������ͺŵ��豸��Ҫ������һ̨��ѧУ���ļ��ֹ�����
Ԫ���������ͺŵ��豸��Ҫ������һ̨��ѧУ���ļ��ֹ�����
��![]() ���ڣ�
���ڣ�![]() ���������£���Ҫ���ذ뾶���Ƿ�Χ������
���������£���Ҫ���ذ뾶���Ƿ�Χ������![]() �ף�Ϊ�˽�Լ�ʽ��������һ����ʡǮ�Ĺ���.
�ף�Ϊ�˽�Լ�ʽ��������һ����ʡǮ�Ĺ���.
����Ŀ��ijУ���꼶�˸����280��ѧ������Ů������������ͬ������С��Ϊ����ѧ�������ʽ���ˮƽ����չ��һ�ε����о����뽫����Ĺ��̲�ȫ.
�ռ����ݣ�
(1)����С��ƻ�ѡȡ40��ѧ�������ʽ������Գɼ���Ϊ�����������ȡ�������У���������___________������ĸ����
A����ȡ���꼶1�ࡢ2���20��ѧ�������ʽ������Գɼ��������
B����ȡ���������ɼ��Ϻõ�ѧ����40��ѧ�������ʽ������Գɼ��������
C�����꼶�а�ѧ�����ѡȡ��Ů����20��ѧ��ѧ�������ʽ������Գɼ��������
�������������ݣ�
��������ȷ������С������40��ѧ�������ʽ������Գɼ����£�
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
�������ݣ����±���ʾ��
2018����꼶����ѧ��ѧ�������ʽ������Գɼ�ͳ�Ʊ�
|
|
|
|
|
|
|
|
|
|
1 | 1 | 2 | 2 | 4 | 5 | 5 | 2 |
�������ݡ��ó�����
����С�齫ͳ�ƺ��������ȥ��ͬ�ھ��꼶��ѧ�������ʽ������Գɼ���ֱ��ͼ�������˶Աȣ�

(2)���ܴ��еõ��Ľ�����_____________�����������________________________________.
(3)������ʦ�ƻ�����2018���ͳ�����ݰ���75�����µ�ͬѧ�μ����ʼ�ǿѵ����Ŀ����ȫ�꼶Լ��________��ͬѧ�μӴ���Ŀ.