Question

【题目】如图，矩形ABCD中，AB=4，AD=3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．

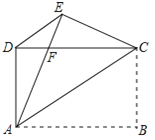
（1）求证：△DEC≌△EDA；

（2）求DF的值；

Answer 1

【答案】见解析

【解析】

试题（1）由矩形和翻折的性质可知AD=CE，DC=EA，根据“SSS”可求得△DEC≌△EDA；

（2）根据勾股定理即可求得

试题解析：（1）由矩形的性质可知△ADC≌△CEA，

∴AD=CE，DC=EA，∠ACD=∠CAE，

在△ADE与△CED中

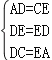
∴△DEC≌△EDA（SSS）；

（2）∵∠ACD=∠CAE，

∴AF=CF，

设DF=x，则AF=CF=4﹣x，

在RT△ADF中，AD2+DF2=AF2，

即32+x2=（4﹣x）2，

解得；x=，

即DF=．