ЬтФПФкШн
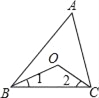
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌвбжЊABЃНBCЃНCAЃН4cmЃЌADЁЭBCгкDЃЌЕуPЁЂQЗжБ№ДгBЁЂCСНЕуЭЌЪБГіЗЂЃЌЦфжаЕуPбиBCЯђжеЕуCдЫЖЏЃЌЫйЖШЮЊ1cm/sЃЛЕуQбиCAЁЂABЯђжеЕуBдЫЖЏЃЌЫйЖШЮЊ2cm/sЃЌЩшЫќУЧдЫЖЏЕФЪБМфЮЊx(s)ЃЎ
(1)ЧѓxЮЊКЮжЕЪБЃЌPQЁЭACЃЛ
(2)ЩшЁїPQDЕФУцЛ§ЮЊ![]() ЃЌЕБ0ЃМxЃМ2ЪБЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЌЕБ0ЃМxЃМ2ЪБЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ЕБ0ЃМxЃМ2ЪБЃЌЧѓжЄЃКADЦНЗжЁїPQDЕФУцЛ§ЃЛ
(4)ЬНЫївдPQЮЊжБОЖЕФдВгыACЕФЮЛжУЙиЯЕЃЌЧыаДГіЯргІЮЛжУЙиЯЕЕФxЕФШЁжЕЗЖЮЇ(ВЛвЊЧѓаДГіЙ§ГЬ)ЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉyЃН
ЃЛЃЈ2ЃЉyЃН![]() ЃЛЃЈ3ЃЉЯъМћНтЮіЃЛЃЈ4ЃЉЕБ
ЃЛЃЈ3ЃЉЯъМћНтЮіЃЛЃЈ4ЃЉЕБ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃМxЁм4ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрНЛЃЎ
ЃМxЁм4ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрНЛЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉШєЪЙPQЁЭACЃЌдђИљОнТЗГЬ=ЫйЖШЁСЪБМфБэЪОГіCPКЭCQЕФГЄЃЌдйИљОн30ЖШЕФжБНЧШ§НЧаЮЕФаджЪСаЗНГЬЧѓНтЃЛЃЈ2ЃЉЕБ0ЃМxЃМ2ЪБЃЌPдкBDЩЯЃЌQдкACЩЯЃЌЙ§ЕуQзїQNЁЭBCгкNЃЌгУxБэЪОГіPDЁЂQNЕФГЄЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЧѓЕУyгыxЕФКЏЪ§ЙиЯЕЪНЃЛЃЈ3ЃЉИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌвЊжЄУїADЦНЗжЁїPQDЕФУцЛ§ЃЌжЛашжЄУїOЪЧPQЕФжаЕуЃЎИљОнЬтвтПЩвджЄУїBP=CNЃЌдђPD=DNЃЌдйИљОнЦНааЯпЕШЗжЯпЖЮЖЈРэМДПЩжЄУїЃЛЃЈ4ЃЉИљОнЬтвтПЩжЊВЛДцдкxЕФжЕЃЌЪЙЕУвдPQЮЊжБОЖЕФдВгыACЯрРыЃЌгЩЃЈ1ЃЉПЩжЊЕБxЃН![]() ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрЧаЃЛЕБЕуQдкABЩЯЪБЃЌ8Ѓ2xЃН
ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрЧаЃЛЕБЕуQдкABЩЯЪБЃЌ8Ѓ2xЃН![]() ЃЌНтЕУxЃН
ЃЌНтЕУxЃН![]() ЃЌЕБxЃН
ЃЌЕБxЃН![]() Лђ
Лђ![]() ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрЧаЃЛИљОнжБЯпгыдВЯрНЛЕФЬѕМўПЩжЊЕБ
ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрЧаЃЛИљОнжБЯпгыдВЯрНЛЕФЬѕМўПЩжЊЕБ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃМxЁм4ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрНЛЃЎ
ЃМxЁм4ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрНЛЃЎ
ЪдЬтНтЮіЃК
(1)ЕБQдкABЩЯЪБЃЌЯдШЛPQВЛДЙжБгкACЃЌ
ЕБQдкACЩЯЪБЃЌгЩЬтвтЕУЃЌBPЃНxЃЌCQЃН2xЃЌPCЃН4ЃxЃЛ
ЁпABЃНBCЃНCAЃН4ЃЌЁрЁЯCЃН60ЁуЃЛ
ШєPQЁЭACЃЌдђгаЁЯQPCЃН30ЁуЃЌ
ЁрPCЃН2CQЃЌЁр4ЃxЃН2ЁС2xЃЌ
ЁрxЃН![]() ЃЛ
ЃЛ
(2)ШчЭМЃЌЕБ0ЃМxЃМ2ЪБЃЌPдкBDЩЯЃЌQдкACЩЯЃЌЙ§ЕуQзїQNЁЭBCгкNЃЛ
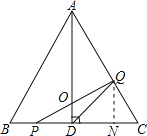
ЁпЁЯCЃН60ЁуЃЌQCЃН2xЃЌ
ЁрQNЃН![]() QCЃН
QCЃН![]() xЃЛ
xЃЛ
ЁпABЃНACЃЌADЁЭBCЃЌ
ЁрBDЃНCDЃН![]() BCЃН2ЃЌ
BCЃН2ЃЌ
ЁрDPЃН2ЃxЃЌ
ЁрyЃН![]() PDЉqQNЃН
PDЉqQNЃН![]() xЃН
xЃН![]() ЃЛ
ЃЛ
(3)ЕБ0ЃМxЃМ2ЪБЃЌдкRtЁїQNCжаЃЌQCЃН2xЃЌЁЯCЃН60ЁуЃЌNCЃНxЃЌ
ЁрBPЃНNCЃЌ
ЁпBDЃНCDЃЌ
ЁрDPЃНDNЃЛ
ЁпADЁЭBCЃЌQNЁЭBCЃЌ
ЁрADЁЮQNЃЌ
ЁрOPЃНOQЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрADЦНЗжЁїPQDЕФУцЛ§ЃЛ
(4)ЯдШЛЃЌВЛДцдкxЕФжЕЃЌЪЙЕУвдPQЮЊжБОЖЕФдВгыACЯрРыЃЌ
гЩ(1)ПЩжЊЃЌЕБxЃН![]() ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрЧаЃЛЕБЕуQдкABЩЯЪБЃЌ8Ѓ2xЃН
ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрЧаЃЛЕБЕуQдкABЩЯЪБЃЌ8Ѓ2xЃН![]() ЃЌНтЕУxЃН
ЃЌНтЕУxЃН![]() ЃЌ
ЃЌ
ЙЪЕБxЃН![]() Лђ
Лђ![]() ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрЧаЃЌ
ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрЧаЃЌ
ЕБ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃМxЁм4ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрНЛЃЎ
ЃМxЁм4ЪБЃЌвдPQЮЊжБОЖЕФдВгыACЯрНЛЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ