题目内容
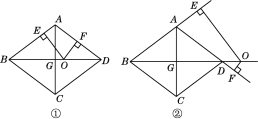
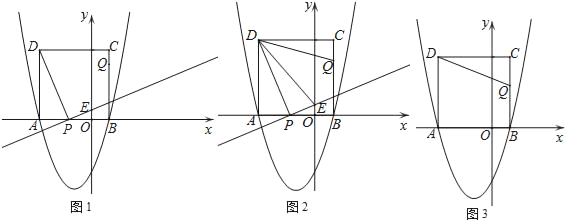
【题目】如图,二次函数y=x2+2x+c的图象与x轴交于点A和点B(1,0),以AB为边在x轴上方作正方形ABCD,动点P从点A出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,同时动点Q从点C出发,以每秒1个单位长度的速度沿CB匀速运动,当点Q到达终点B时,点P停止运动,设运动时间为t秒.连接DP,过点P作DP的垂线与y轴交于点E.
(1)求二次函数的解析式及点A的坐标;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,并求出这个最大值;
(3)在P,Q运动过程中,求当△DPE与以D,C,Q为顶点的三角形相似时t的值;
(4)是否存在t,使△DCQ沿DQ翻折得到△DC′Q,点C′恰好落在抛物线的对称轴上?若存在,请求出t的值;若不存在,请说明理由.
【答案】(1)y=x2+2x﹣3,点A的坐标为(﹣3,0);
(2)点P位于AO的中点时,线段OE的长有最大值![]() ;
;
(3)t=1或3或![]() ,
,
(4)存在t=![]() .
.
【解析】试题分析:(1)先将点B的坐标代入解析式求得c的值确定二次函数解析式,令y=0即可求得A点坐标.
(2)由DP⊥PE证得△DAP∽△POE,用比例式表示出y与t的关系,根据函数图象的性质可求得OE的最大值.
(3)需要分类讨论:根据t的不同取值得出相似三角形,再由相似的性质可得t的取值.
(4)先证明△DCQ≌DC′Q,从而得到∠CDQ=∠C′DQ,DC′=DC=4,再得出∠CDQ=30°,即可求得满足条件的t值.
解:(1)把B(1,0)代入y=x2+2x+c得c=﹣3,
∴y=x2+2x﹣3,
由x2+2x﹣3=0得x1=﹣3,x2=1,
∴点A的坐标为(﹣3,0).
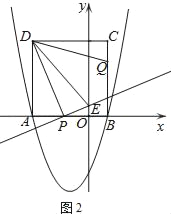
(2)如图(2),由正方形ABCD得AD=AB=4,
由DP⊥PE证得△DAP∽△POE,
∴![]() ,设OE=y,则
,设OE=y,则![]() ,
,
∴y=![]() =﹣(t﹣
=﹣(t﹣![]() )2+
)2+![]() ,
,
∵a=﹣1<0,
∴当t=![]() 时(属于0<t<
时(属于0<t<![]() )时,y最大=
)时,y最大=![]() ,此时2t=
,此时2t=![]() ,即点P位于AO的中点时,
,即点P位于AO的中点时,
∴线段OE的长有最大值![]() .
.
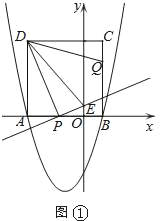
(3)①如图①,当0<t<![]() 时,△DPE∽△DCQ,
时,△DPE∽△DCQ,
∴![]() .又△ADP∽△OPE,
.又△ADP∽△OPE,
∴![]() ,
,
∴![]() .即
.即![]() ,解得t=1,
,解得t=1,
经检验:t=1是原方程的解.
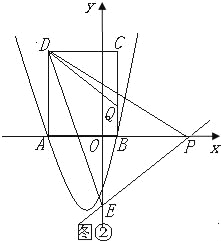
②如图②,当![]() 时,同理证得△ADP∽△OPE,
时,同理证得△ADP∽△OPE,
∴![]() ,
,
即![]() ,解得t=3.经检验:t=3是原方程的解.
,解得t=3.经检验:t=3是原方程的解.
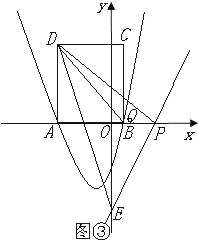
③如图③,当![]() 时,△DPE∽△QCD,
时,△DPE∽△QCD,
∴![]() ,
,
同理得![]() ,
,
∴![]() .即
.即![]() ,解得t1=
,解得t1=![]() t2=
t2=![]() (经检验:舍去t2=
(经检验:舍去t2=![]() ),
),
综上所述,t=1或3或![]() ,
,
(4)存在t=![]() .
.
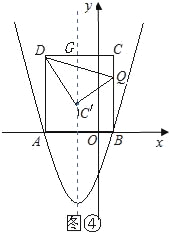
理由如下:如图
由△DCQ沿DQ翻折得△DC′Q,则△DCQ≌△DC′Q,
∴∠CDQ=∠C′DQ,DC′=DC=4,
设抛物线的对称轴交DC于G,则DG=2.在Rt△DC′G中,
∵C′D=2DG,
∴∠C′DG=60°,
∴∠CDQ=![]() ×60°=30°,
×60°=30°,
∴CQ=![]() ,即t=
,即t=![]() .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案