题目内容
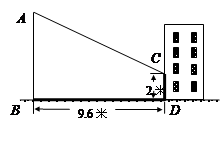
如图,大楼AB、CD和大树EF的底端B、D、F在同一直线上,BF=FD=10米,AB=16米,某人在楼顶A处测得点C的仰角为22°,测得点E的俯角为45°.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
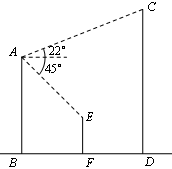
(1)求大树EF的高度;
(2)求大楼CD的高度.

(1)求大树EF的高度;
(2)求大楼CD的高度.
(1)6米;(2)24米
试题分析:(1)作AH⊥CD,垂足为H,作EG⊥AB,垂足为G,先根据等腰直角三角形的性质求得AG=GE=10,即可求得结果;
(2)在Rt△ACH中,根据∠CAH的正切函数即可求得CH的长,从而求得结果.
(1)作AH⊥CD,垂足为H,作EG⊥AB,垂足为G
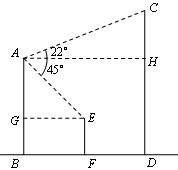
由题意知,EG=10,∠EAG=45°,∠AGE=90°,
∴AG=GE=10.
∴EF=GB=AB-AG=16-10=6(米);
(2)在Rt△ACH中,∠CAH=22°,
CH=AH·tan22°=20×0.40=8(米).
∴CD=CH+HD=16+8=24(米)
答:大树EF的高度是6米,大楼CD的高度是24米.
点评:解直角三角形的应用是中考必考题,一般难度不大,正确作出辅助线构造直角三角形是解题关键.

练习册系列答案
相关题目
 (万件)与销售单位
(万件)与销售单位 (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系. (万元)关于销售单价
(万元)关于销售单价
 , y=
, y=

 km的地方。
km的地方。

 地出发前往
地出发前往 地,且两人到达
地,且两人到达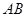 之间往返行驶,甲的速度为32
之间往返行驶,甲的速度为32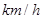 ,乙的速度为18
,乙的速度为18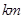 ,则
,则