题目内容
甲乙两人骑摩托车同时从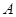
地出发前往
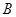地，且两人到达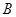地后各自按原速度返回，且不停地在
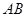之间往返行驶，甲的速度为32
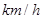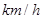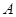，乙的速度为18，当乙车由至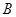多次后，甲车两次追上乙车，且第二次追上乙时是在乙车从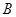地向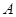地行驶的途中，且他们此时距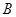地的距离为10
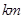，则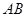两地相距__________．
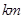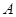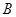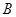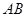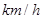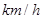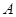地出发前往地，且两人到达地后各自按原速度返回，且不停地在之间往返行驶，甲的速度为32，乙的速度为18，当乙车由至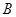多次后，甲车两次追上乙车，且第二次追上乙时是在乙车从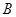地向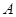地行驶的途中，且他们此时距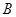地的距离为10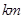，则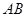两地相距__________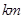．70
解：设AB间的距离为s千米，第二次甲追上乙时所用的时间为t小时
第二次甲追上乙时 乙行驶的距离至少有3s+10
甲行驶的距离至少有7s+10
所以有： 32t-18t=4s
t=7s/2
但第二次甲追上乙时，他们距B地10千米， 这说明 s>10
于是得到：t>20/7
以乙行行驶过程计算（相比甲过程计算简单）：（1）假设3s+10与甲相遇，有3s+10=18t
解之：t=4/3(舍) （2）前面不成立就假设5s+10与甲相遇，有5s+10=18t 解之：t=20
(3)继续假设7s+10与甲相遇，则有7st+10=18t 解之：t为负数 。 以后都为负数。
所以：s=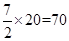
第二次甲追上乙时 乙行驶的距离至少有3s+10
甲行驶的距离至少有7s+10
所以有： 32t-18t=4s
t=7s/2
但第二次甲追上乙时，他们距B地10千米， 这说明 s>10
于是得到：t>20/7
以乙行行驶过程计算（相比甲过程计算简单）：（1）假设3s+10与甲相遇，有3s+10=18t
解之：t=4/3(舍) （2）前面不成立就假设5s+10与甲相遇，有5s+10=18t 解之：t=20
(3)继续假设7s+10与甲相遇，则有7st+10=18t 解之：t为负数 。 以后都为负数。
所以：s=
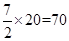
练习册系列答案
相关题目
的最小覆盖圆就是以线段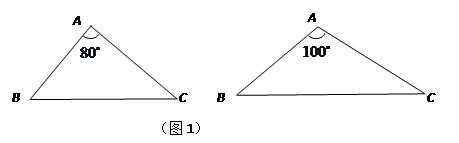
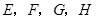（其位置如图2所示），现拟建一个电视信号中转站，为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（距离越小，所需功率越小），此中转站应建在何处？请说明理由．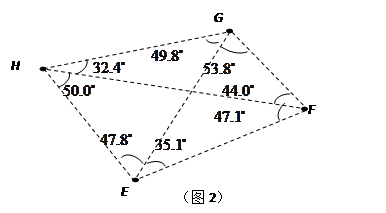
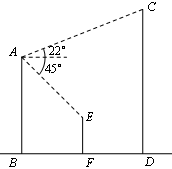
分别表示学校、小明家、小红家，已知学校在小明家的南偏东
，小红家在小明家正东，小红家在学校北偏东
，则
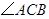等于（ ）
、
、
、
、
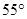
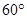
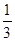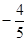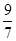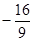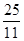…，请你按这种规律写出第七个数 。
，
，
”、“
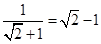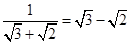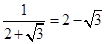
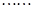
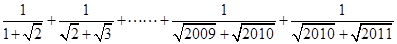
”定义新运算：对于任意实数a，b，都有a
