题目内容
【题目】正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于F,则EF的长为 . 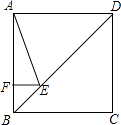
【答案】4﹣2 ![]()
【解析】解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,
∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,
在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠DAE=∠AED,
∴AD=DE=4,
∵正方形的边长为4,
∴BD=4 ![]() ,
,
∴BE=BD﹣DE=4 ![]() ﹣4,
﹣4,
∵EF⊥AB,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴EF= ![]() BE=
BE= ![]() ×(4
×(4 ![]() ﹣4)=4﹣2
﹣4)=4﹣2 ![]() .
.
所以答案是:4﹣2 ![]() .
.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目