题目内容
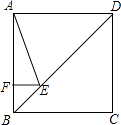
【题目】如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与点C重合,折痕EF交AD于点E,交BC于点F,交AC于点O,连结AF,CE.
(1)求证:四边形AFCE是菱形;
(2)若AE=8,△ABF的面积为9,求AB+BF的值.

【答案】(1)见解析;(2)10.
【解析】
(1)当顶点A与C重合时,折痕EF垂直平分AC,由OA=OC,得∠AOE=∠COF=90°,由题意得AD∥BC,∠EAO=∠FCO,可证明△AOE≌△COF,从而得出∴四边形AFCE是菱形.
(2)根据四边形AFCE是菱形,得出AF=AE=8,在Rt△ABF中,利用勾股定理得AB2+BF2=AF2,AB2+BF2=82,即可得出(AB+BF)2-2ABBF=64①,根据△ABF的面积为9,可求得ABBF=18②,再由①、②得:(AB+BF)2=100,得出AB+BF=10.
(1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴四边形AFCE是平行四边形,
又∵EA=EC
∴平行四边形AFCE是菱形.
(2)∵四边形AFCE是菱形,
∴AF=AE=8,在Rt△ABF中,AB2+BF2=AF2,
∴AB2+BF2=64,∴(AB+BF)2-2AB·BF=64①,
∵△ABF的面积为9,
∴![]() AB·BF=9,
AB·BF=9,
∴AB·BF=18②,
由①、②得:(AB+BF)2=100,
∵AB+BF>0,
∴AB+BF=10.

 名校课堂系列答案
名校课堂系列答案【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x | 20 | 25 | 30 | 50 |
销售量y | 15 | 12 | 10 | 6 |
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
【题目】声音在空气中传播的速度y(m/s)(简称音速)与气温x(℃)的关系如下表:
气温x(℃) | 0 | 5 | 10 | 15 | 20 |
音速y(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)这一变化过程中,自变量和因变量各是什么?
(2)音速y(m/s)与气温x(℃)之间的关系式;
(3)气温x=22℃时,某人看到烟花烯放5s后才听到声音,那么此人与燃烟花的所在地约相距多远?
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 18 | 0.12 |
2≤x<3 | a | m |
3≤x<4 | 45 | 0.3 |
4≤x<5 | 36 | n |
5≤x<6 | 21 | 0.14 |
合计 | b | 1 |
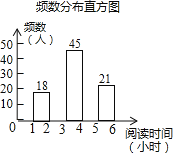
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整(画图后请标注相应的频数).