题目内容
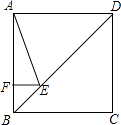
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.

(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
【答案】
【1】(1)∵四边形ABCD是平行四边形∴AB=DC,AD=BC,∠A=∠C. … 2分
∵点E,F分别为边AB,CD的中点
∴![]() ∴
∴![]()
∴△ADE≌△CBF![]()
【2】(2)∵AB=DC,AE = CF,∴DF=BE,
又∵四边形ABCD是平行四边形,∴DC∥AB,
∴四边形BFDE是平行四边形
∵AD⊥BD,∴![]() ,∵点E是AB中点,∴
,∵点E是AB中点,∴![]() ,
,
∴□BFDE是菱形…
【解析】(1)根据平行四边形的性质即可证出△ADE与△CBF全等;(2)根据直角三角形斜边上的中线等于斜边的一半及平行四边形的判定即可证出四边形BFDE是菱形.
解:(1)证明:在平行四边形ABCD中,∠A=∠C,AD=BC,
∵E、F分别为AB、CD的中点,
∴AE=CF.
在△AED和△CFB中,

∴△AED≌△CFB(SAS);
(2)菱形,若AD⊥BD,则四边形BFDE是菱形.
证明:∵AD⊥BD,
∴△ABD是直角三角形,且∠ADB=90°.
∵E是AB的中点,
∴DE=![]() AB=BE.
AB=BE.
∵在ABCD中,E,F分别为边AB,CD的中点,
∴EB∥DF且EB=DF,
∴四边形BFDE是平行四边形.
∴四边形BFDE是菱形.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】声音在空气中传播的速度y(m/s)(简称音速)与气温x(℃)的关系如下表:
气温x(℃) | 0 | 5 | 10 | 15 | 20 |
音速y(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)这一变化过程中,自变量和因变量各是什么?
(2)音速y(m/s)与气温x(℃)之间的关系式;
(3)气温x=22℃时,某人看到烟花烯放5s后才听到声音,那么此人与燃烟花的所在地约相距多远?