题目内容
如图,一块直角三角形木板△ABC,将其在水平面上沿斜边AB所在直线按顺时针方向翻滚,使它滚动到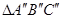 的位置,若BC=1cm,AC=
的位置,若BC=1cm,AC=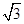 cm,则顶点A运动到
cm,则顶点A运动到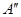 时,点A所经过的路径是 cm.
时,点A所经过的路径是 cm. 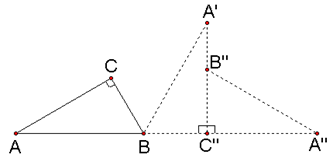
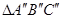 的位置,若BC=1cm,AC=
的位置,若BC=1cm,AC=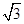 cm,则顶点A运动到
cm,则顶点A运动到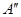 时,点A所经过的路径是 cm.
时,点A所经过的路径是 cm. 
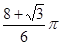
从图中我们可以看出,顶点A运动到A″时,点A所经过的路径长,是两段弧长,一段是以点B为圆心,AB为半径,圆心角是120度的弧,第二次转动是以点C′为圆心,AC为半径,圆心角是90°的弧长.根据弧长公式就可得出点A所经过的路径长.
解:BC=1cm,AC=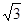 cm,
cm,
∴AB=2,∠A=30°,∠B=60°.
∴点A运动的第一段弧长=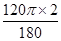 =
= .
.
第二段弧长=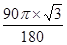 =
=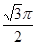 .
.
∴顶点A运动到A″时,点A所经过的路径= +
+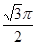 =
=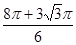 .
.
本题的关键是读题,并利用弧长公式计算.
解:BC=1cm,AC=
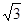 cm,
cm,∴AB=2,∠A=30°,∠B=60°.
∴点A运动的第一段弧长=
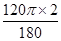 =
= .
.第二段弧长=
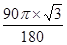 =
=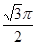 .
.∴顶点A运动到A″时,点A所经过的路径=
 +
+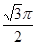 =
=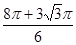 .
.本题的关键是读题,并利用弧长公式计算.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
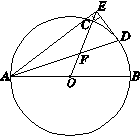
 ,求
,求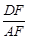 的值.
的值.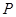 ,军舰
,军舰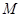 停泊在雷达站
停泊在雷达站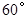 方向36海里处,另一艘军舰
方向36海里处,另一艘军舰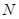 位于军舰
位于军舰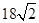 海里.求:
海里.求: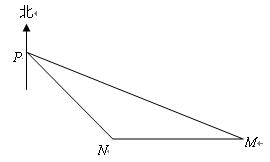
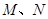 的距离.(结果保留根号)
的距离.(结果保留根号) ,OD=20.(1)求∠ABC的度数;(2)连接BE,求线段BE的长
,OD=20.(1)求∠ABC的度数;(2)连接BE,求线段BE的长
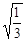 -
- +
+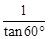 +(sin45°)0
+(sin45°)0 ,求c及∠B.
,求c及∠B.


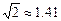 ,sin37°≈0.60,cos37°≈0.80)
,sin37°≈0.60,cos37°≈0.80) 