题目内容
如图，AC是⊙O的直径，AB与⊙O相切于点A，四边形ABCD是平行四边形，BC交⊙O于点E．
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为5cm，弦CE的长为8cm，求AB的长．
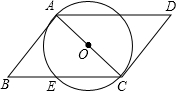
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为5cm，弦CE的长为8cm，求AB的长．
（1）直线CD与⊙O相切，
理由：∵AC是⊙O的直径，AB与⊙O相切于点A，
∴AC⊥AB，
又∵四边形ABCD是平行四边形，
∴AB∥CD，
∴AC⊥CD，
∴直线CD与⊙O相切；
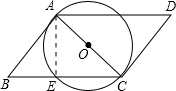（2）连接AE，
∵AC为圆的直径，
∴∠AEC=90°，
∵AB与⊙O相切于点A，
∴AC⊥AB，
∴∠BAC=90°，
∴∠AEC=∠BAC=90°，
又∵∠ACE=∠BCA，
∴△CAE∽△CBA，
∴
=
①，
又∵AC=2AO=10cm，EC=8cm，
∴根据勾股定理可得，AE=
=6（cm），
代入关系式①得，
=
，
解得AB=7.5cm．
理由：∵AC是⊙O的直径，AB与⊙O相切于点A，
∴AC⊥AB，
又∵四边形ABCD是平行四边形，
∴AB∥CD，
∴AC⊥CD，
∴直线CD与⊙O相切；
（2）连接AE，∵AC为圆的直径，
∴∠AEC=90°，
∵AB与⊙O相切于点A，
∴AC⊥AB，
∴∠BAC=90°，
∴∠AEC=∠BAC=90°，
又∵∠ACE=∠BCA，
∴△CAE∽△CBA，
∴
| CE |
| AE |
| AC |
| AB |
又∵AC=2AO=10cm，EC=8cm，
∴根据勾股定理可得，AE=
| AC2-EC2 |
代入关系式①得，
| 8 |
| 6 |
| 10 |
| AB |
解得AB=7.5cm．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
