题目内容
如图，在等腰三角形ABC中，AB=AC，O为AB上一点，以O为圆心、OB长为半径的圆交BC于D，DE⊥AC交AC于E．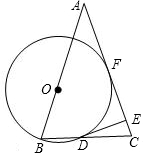
求证：DE是⊙O的切线．
求证：DE是⊙O的切线．
证明：连接OD，如图，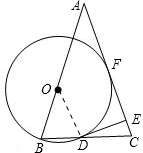
则OB=OD
∴∠OBD=∠ODB，
又∵AB=AC
∴∠OBD=∠C
∴∠ODB=∠C
∴OD∥AC
又∵DE⊥AC
∴OD⊥DE
∴DE是⊙O的切线．
则OB=OD
∴∠OBD=∠ODB，
又∵AB=AC
∴∠OBD=∠C
∴∠ODB=∠C
∴OD∥AC
又∵DE⊥AC
∴OD⊥DE
∴DE是⊙O的切线．
练习册系列答案
名校课堂系列答案
相关题目
于E，且点O在AB上．
