题目内容
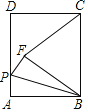
【题目】如图，在矩形ABCD中，AB＝5，BC＝6，P为AD上一动点，把△ABP沿BP翻折，使点A落在点F处，连接CF，若BF＝CF，则AP的长为_____．
【答案】
【解析】
过点F作EN∥DC交BC于点N，交AD于点E，设AP＝x，则PF＝x，得出（3﹣x）2+12＝x2，解方程即可得解．
解：过点F作EN∥DC交BC于点N，交AD于点E，
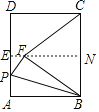
∵四边形ABCD是矩形，
∴∠A＝∠D＝∠DCB＝90°，
∴FN⊥BC，FE⊥AD，
∵BF＝CF，BC＝6，
∴CN＝BN＝3，
由折叠的性质可知，AB＝BF＝5，AP＝PF，
∴
，
∴EF＝EN﹣FN＝5﹣4＝1，
设AP＝x，则PF＝x，
∵PE2+EF2＝PF2，
∴（3﹣x）2+12＝x2，
解得，
，
故答案为：．
练习册系列答案
相关题目
【题目】水果店以每箱60元新进一批苹果共400箱，为计算总重量，从中任选30箱苹果称重，发现每箱苹果重量都在10千克左右，现以10千克为标准，超过10千克的数记为正数，不足10千克的数记为负数，将称重记录如下：
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
（1）求30箱苹果的总重量
（2）若每千克苹果的售价为10元，则卖完这批苹果共获利多少元
