Question

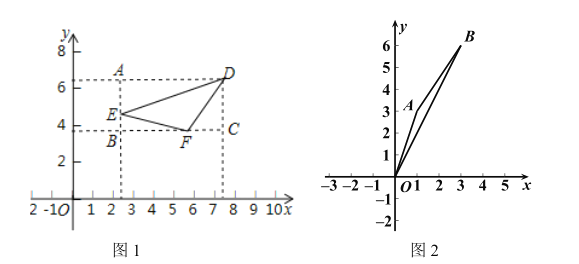
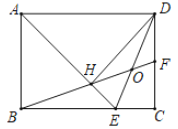
【题目】如图1，在矩形ABCD中，E是CB延长线上一个动点，F、G分别为AE、BC的中点，FG与ED相交于点H．

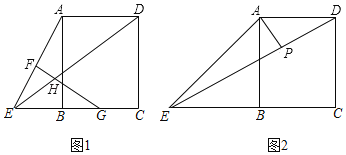
（1）求证：HE＝HG；

（2）如图2，当BE＝AB时，过点A作AP⊥DE于点P，连接BP，求PQ与PB的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）PQPB，理由见解析．

【解析】

（1）连接AG，并延长AG交DC的延长线于M，连接EM，G为BC的中点，根据矩形的性质得出∠ABG=∠DCB=90°，根据全等三角形的判定得出△ABG≌△MCG，根据全等三角形的性质得出GA=GM，求出FG∥EM，根据平行线的性质得出∠HGE=∠MEC，求出△DEC≌△MEC，根据全等三角形的性质得出∠DEC=∠MEC，求出∠HEG=∠HGE即可；

（2）过点B作BQ⊥BP交DE于Q，求出∠APE=∠ABE=90°，∠BEQ=∠BAP，∠EBQ=∠ABP，根据全等三角形的判定得出△BEQ≌△BAP，根据全等三角形的性质得出BQ=BP，PA=QE，求出△PBQ是等腰直角三角形，即可得出答案．

（1）证明：连接AG，并延长AG交DC的延长线于M，连接EM，

∵G为BC的中点，

∴BG＝CG，

∵四边形ABCD是矩形，

∴∠ABG＝∠DCB＝90°，

∴∠ABG＝∠MCG＝90°，

在△ABG和△MCG中，

，

∴△ABG≌△MCG(ASA)，

∴GA＝GM，

∵F为AE的中点，

∴FA＝FE，

∴FG是△AEM的中位线，

∴FG∥EM，

∴∠HGE＝∠MEC，

在△DCE和△MCE中，

，

∴△DEC≌△MEC(SAS)，

∴∠DEC＝∠MEC，

∵∠HGE＝∠MEC，

∴∠HEG＝∠HGE，

∴HE＝HG；

（2）答：PQPB

理由：过点B作BQ⊥BP交DE于Q，则∠QBP＝90°，

∵AP⊥DE，四边形ABCD是矩形，

∴∠APE＝∠ABE＝90°，

∵∠APO＋∠AOP＋∠BAP＝180°，∠EOB＋∠ABE＋∠BEP＝180°，∠AOP＝∠EOB，

∴∠BEQ＝∠BAP，

∵∠QBP＝∠ABE＝90°，

∴∠EBQ＝∠ABP＝90°﹣∠ABQ，

在△ABP和△EBQ中，

，

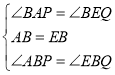∴△BEQ≌△BAP(ASA)，

∴BQ＝BP，PA＝QE，

∴△PBQ是等腰直角三角形，

∴PQPB．