题目内容
【题目】(发现)
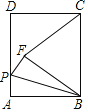
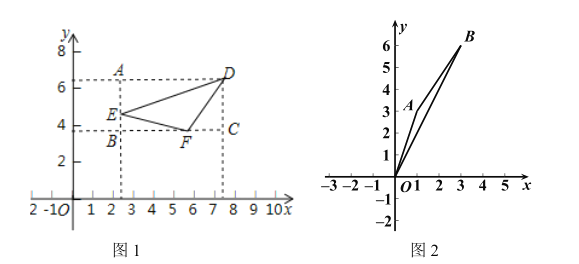
(1)如图1,在ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F.求证:△AOE≌△COF;

(探究)
(2)如图2,在菱形ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F,若AC=4,BD=8,求四边形ABFE的面积.
(应用)
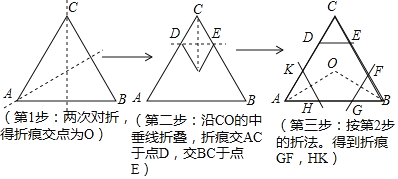
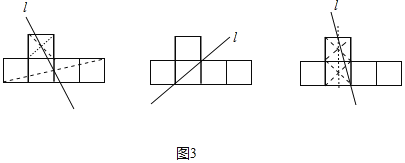
(3)如图3,边长都为1的5个正方形如图摆放,试利用无刻度的直尺,画一条直线平分这5个正方形组成的图形的面积.(要求:保留画图痕迹)
【答案】(1)见解析 (2)8 (3)见解析
【解析】
(1)根据ASA证明三角形全等即可.
(2)证明S四边形ABFE=S△ABC可得结论.
(3)利用中心对称图形的性质以及数形结合的思想解决问题即可(答案不唯一).
(1)【发现】证明:如图1中,∵四边形ABCD是平行四边形,
∴AO=OC,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
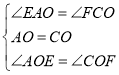 ,
,
∴△AOE≌△COF(ASA).
(2)【探究】解:如图2中,由(1)可知△AOE≌△COF,
∴S△AOE=S△COF,
∴S四边形ABFE=S△ABC,
∵四边形ABCD是菱形,
∴S△ABC=![]() S菱形ABCD,
S菱形ABCD,
∵S菱形ABCD=![]() ACBD=
ACBD=![]() ×4×8=16,
×4×8=16,
∴S四边形ABFE=![]() ×16=8.
×16=8.
(3)【应用】
①找出上面小正方形的对角线交点,以及下面四个小正方形组成的矩形的对角线交点,连接即可;
②连接下面左边数第二个小正方形右上角和左下角的顶点;
③分别找出第二列两个小正方形的对角线交点,并连接,与最上面的小正方形最上面的边交于一点,把这个点与图形底边中点连接即可.
如图3中,直线l即为所求(答案不唯一).

练习册系列答案
相关题目