题目内容
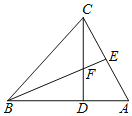
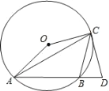
【题目】如图,△ABC是⊙O内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O切线交AB延长线于点D.
(1)求证:CD=CB;(2)如果⊙O的半径为![]() ,求AC的长.
,求AC的长.
【答案】(1)证明见解析;(2)![]() +1.
+1.
【解析】
(1)首先连接OB,则∠AOB=2∠ACB=2×45°=90°,由∠AOC=150°,易得△OBC是等边三角形,又由过点C作⊙O的切线交AB的延长线于点D,易求得∠CBD=∠D=75°,继而证得结论;
(2)由⊙O的半径为![]() ,可求得AB=2,CD=BC=OC=
,可求得AB=2,CD=BC=OC=![]() ,易证得△DBC∽△DCA,然后由相似三角形的对应边成比例,求得答案.
,易证得△DBC∽△DCA,然后由相似三角形的对应边成比例,求得答案.
(1)连接OB,则∠AOB=2∠ACB=2×45°=90°,∵OA=OB,∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,∴∠OCA=∠OAC=15°,∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,∴∠BOC=∠OBC=60°,∴∠CBD=180°﹣∠OBA﹣∠OBC=75°,
∵CD是⊙O的切线,∴OC⊥CD,
∴∠D=360°﹣∠OBD﹣∠BOC﹣∠OCD=360°﹣(60°+75°)﹣60°﹣90°=75°,
∴∠CBD=∠D,∴CB=CD;
(2)在Rt△AOB中,AB=![]() OA=
OA=![]() ×
×![]() =2,∵CD是⊙O的切线,∴∠DCB=∠CAD,
=2,∵CD是⊙O的切线,∴∠DCB=∠CAD,
∵∠D是公共角,∴△DBC∽△DCA,∴![]() ,∴CD2=ADBD=BD(BD+AB),
,∴CD2=ADBD=BD(BD+AB),
∵CD=BC=OC=![]() ,∴2=BD(2+BD),解得:BD=
,∴2=BD(2+BD),解得:BD=![]() ﹣1,∴AC=AD=AB+BD=
﹣1,∴AC=AD=AB+BD=![]() +1.
+1.

 阅读快车系列答案
阅读快车系列答案【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”, “5”,“6”的四张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
奖项 | 一等奖 | 二等奖 | 三等奖 |
|x| | |x|=4 | |x|=3 | 1 |
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)求出每次抽奖获奖的概率?
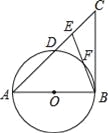
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
【题目】“文明礼仪”在人们长期生活和交往中逐渐形成,并以风俗、习惯等方式固定下来的.我们作为具有五千年文明史的“礼仪之邦”,更应该用文明的行为举止, 合理的礼仪来待人接物.为促进学生弘扬民族文化、展示民族精神,某学校开展“文明礼仪”演讲比赛,八年级(1)班,八年级(2)班各派出 5 名选手参加比赛,成绩如图所示.
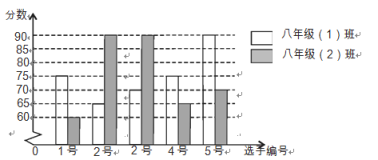
(1)根据图,完成表格:
平均数(分) | 中位数(分) | 极差(分) | 方差 | |
八年级(1)班 | 75 |
| 25 |
|
八年级(2)班 | 75 | 70 |
| 160 |
(2)结合两班选手成绩的平均分和方差,分析两个班级参加比赛选手的成绩;
(3)如果在每班参加比赛的选手中分别选出3人参加决赛,从平均分看,你认为哪个班的实力更强一些? 说明理由.