Question

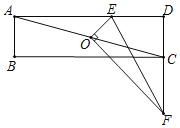
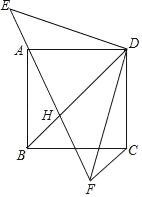
【题目】如图示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BD相交于点H，连接CF．

①求证：△DAE≌△DCF．

②求证：AH2=AE2+HF2．

Answer 1

【答案】①详见解析；②详见解析．

【解析】

由正方形ABCD与等腰直角三角形DEF,得到两对边相等,一对直角相等,利用SAS即可得证;

连接CH,求证△ADH≌△CDH和△ADE≌△CDF,再根据题目条件得出为直角三角形，即可求解.

证明：①∵正方形ABCD，等腰直角三角形EDF，

∴∠ADC=∠EDF=90°，AD=CD，DE=DF，

∴∠ADE+∠ADF=∠ADF+∠CDF，

∴∠ADE=∠CDF，

在△ADE和△CDF中，

，

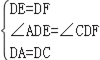∴△ADE≌△CDF（SAS）；

②连接CH，

∵DA=DC，∠ADH=∠CDH=45°，DH=DH，

∴△ADH≌△CDH（SAS），

∴AH=CH，

∵△ADE≌△CDF（SAS），

∴∠E=∠DFC=45°，

∵∠DFE=45°，

∴∠HFC=90°，

∴CH2=FH2+CF2，

∴AH2=FH2+CF2．