题目内容
【题目】在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.

(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;
(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.
【答案】(1)证明见解析(2)证明见解析(3)2
【解析】
感知:先利用矩形性质得: ∠D=∠C=90°,再利用同角的余角相等得: ∠DAE=∠FEC,根据已知边的长度计算出AD=CE=3,则由ASA证得: △ADE≌△ECF;
探究:利用两角相等证明△PDE∽△ECF;
应用:作辅助线,构建如图②一样的相似三角形,利用探究得: △PDE∽△EGF,则![]() ,所以
,所以![]() ,再利用△PEF的面积是3,列式可得:PE·EF=6,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
,再利用△PEF的面积是3,列式可得:PE·EF=6,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
(1)证明:感知:如图①,∵四边形ABCD为矩形,
∴∠D=∠C=90°,
∴∠DAE+∠DEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠DEA+∠FEC=90°,
∴∠DAE=∠FEC,
∵DE=1,CD=4,
∴CE=3,
∵AD=3,
∴AD=CE,
∴△ADE≌△ECF(ASA)
(2)探究:如图②,∵四边形ABCD为矩形,
∴∠D=∠C=90°,
∴∠DPE+∠DEP=90°,
∵EF⊥PE,
∴∠PEF=90°,
∴∠DEP+∠FEC=90°,
∴∠DPE=∠FEC,
∴△PDE∽△ECF
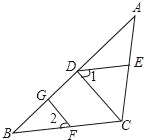
(3)应用:解:如图③,过F作FG⊥DC于G,
∵四边形ABCD为矩形,
∴AB∥CD,
∴FG=BC=3,
∵PE⊥EF,
∴S△PEF=![]() PEEF=3,
PEEF=3,
∴PEEF=6,
同理得:△PDE∽△EGF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴EF=3PE,
∴3PE2=6,
∴PE=±![]() ,
,
∵PE>0,
∴PE=![]() ,
,
在Rt△PDE中,由勾股定理得:PD=![]() =1,
=1,
∴AP=AD﹣PD=3﹣1=2.