Question

【题目】如图，已知正方形ABCD中，E、F分别是正方形AD、CD边上的点，且∠EBF=45°，对角线AC交BE,BF于M,N，对于以下结论，正确的是（ ）①AE+CF=FE②△ABE≌△BCF③AM2+CN2=MN2④△EFD的周长等于2AB

A.①②③B.①②④C.①③④D.①②③④

Answer 1

【答案】C

【解析】

延长DA至点H，使AH=CF，连接BH，证明△BCF≌△BAH，△HBE≌△FBE即可判断①②④，然后作BG⊥EF，连接MG，NG，证明△BAM≌△BGM，△BCN≌△BGN，根据勾股定理即可判定③.

解：延长DA至点H，使AH=CF，连接BH，

∵四边形ABCD为正方形，

∴AB=BC，∠BAH=∠BCF=90°，

在△BCF和△BAH中

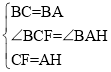
∴△BCF≌△BAH（SAS），

∴BF=BH，∠CBF=∠ABH，CF=AH，

∵∠EBF=45°，

∴∠ABE+∠CBF=45°，则∠HBE=45°，

在△HBE和△FBE中

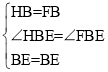
∴△HBE≌△FBE（SAS），

∴HE=HF，即CF+AE=EF，故①正确；

∵题上没有说明AE=CF，故②错误；

△EFD的周长=ED+EF+FD=ED+AE+CF+FD=2AB，故④正确；

作BG⊥EF，连接MG，NG，

∵△HBE≌△FBE，

∴∠BEA=∠BEG，从而得到△BAE≌△BGE，△BCF≌△BGF，

∴∠ABE=∠GBE，∠CBF=∠GBF，从而得到△BAM≌△BGM，△BCN≌△BGN，

∴AM=GM，CN=NG，∠BAM=∠BGM，∠BCN=∠BGN，

∵∠BAM+∠BCN=90°，

∴∠MGN=90°，

∴GM2+GN2=MN2

∴AM2+CN2=MN2，故③正确；

故正确的是①③④，故选C.